题目内容
1.数列{an}的前n项和为${S_n}={2^{n+1}}-2$,数列{bn}是首项为a1,公差为d(d≠0)的等差数列,且b1,b3,b9成等比数列.(1)求数列{an}与{bn}的通项公式;
(2)若${c_n}=\frac{2}{{{b_{n+2}}•{{log}_2}{a_n}}}$,数列{cn}的前n项和为 Tn,求证:${{T}_n}<\frac{3}{4}$.
分析 (1)运用数列的通项和求和的关系,将n换为n-1,作差即可得到所求数列{an}的通项;再由等比数列的中项的性质和等差数列的通项公式,解方程可得公差为2,即可得到数列{bn}的通项;
(2)求得${c_n}=\frac{2}{{{b_{n+2}}•{{log}_2}{a_n}}}$=$\frac{2}{2(n+2)•n}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),再由裂项相消求和及不等式的性质,即可得证.
解答 解:(1){an}的前n项和为${S_n}={2^{n+1}}-2$,
可得a1=S1=4-2=2,
又Sn-1=2n-2,(n>1),
相减可得an=2n,对n=1也成立.
即有an=2n,(n∈N*);
由题意可得bn=a1+(n-1)d=2+(n-1)d,
b1,b3,b9成等比数列,可得b1b9=b32,
即为2(2+8d)=(2+2d)2,
解得d=2(0舍去),
可得bn=2n,(n∈N*);
(2)证明:${c_n}=\frac{2}{{{b_{n+2}}•{{log}_2}{a_n}}}$=$\frac{2}{2(n+2)•n}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
前n项和为Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<$\frac{3}{4}$.
点评 本题考查等差数列和等比数列的通项公式的运用,考查数列的通项和求和的关系,同时考查数列的求和方法:裂项相消求和,以及不等式的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案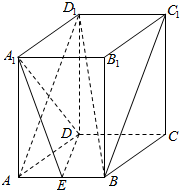 长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点. 如图,已知圆柱的高为4,AA1,BB1,CC1是圆柱的三条母线,AB是底面圆O的直径,AC=3,AB=5.
如图,已知圆柱的高为4,AA1,BB1,CC1是圆柱的三条母线,AB是底面圆O的直径,AC=3,AB=5.