题目内容
函数y=
的定义域是（ ）
| 1-x2 |
| A、{x|-1＜x＜1} |
| B、{x|x≤-1} |
| C、{x|x≥1} |
| D、{x|-1≤x≤1} |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由根式内部的代数式大于等于零，然后求解二次不等式得函数的定义域．
解答：
解：要使函数有意义，必须1-x2≥0，解得-1≤x≤1
故函数的定义域为：{x|-1≤x≤1}．
故选：D．
故函数的定义域为：{x|-1≤x≤1}．
故选：D．
点评：本题考查了函数的定义域及其求法，考查了不等式的解法，是基础题．
练习册系列答案
相关题目
| A | 0 4 |
| A | 1 4 |
| A | 2 4 |
| A | 3 4 |
| A | 4 4 |
| A、16 | B、15 | C、65 | D、64 |
满足M⊆{a1，a2，a3}，且M∩{a1，a2，a3}={a3}的集合M的子集个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
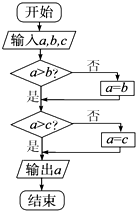如图所示的算法中，令a=tan θ，b=sin θ，c=cos θ，若在集合{θ|-