题目内容
20.三角形ABC中,角A,B,C所对边分别为a,b,c,已知b2+c2-a2=$\sqrt{3}$bc,且a=1,则三角形ABC外接圆面积为π.分析 利用余弦定理表示出cosA,将已知等式代入求出cosA的值,根据A为三角形内角,可求sinA的值,再利用正弦定理即可求出外接圆半径,利用圆的面积公式即可计算得解.
解答 解:∵b2+c2-a2=$\sqrt{3}$bc,且a=1,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}bc}{2bc}$=$\frac{\sqrt{3}}{2}$,
∵A为三角形内角,
∴sinA=$\frac{1}{2}$,
∴设三角形ABC外接圆半径为R,根据正弦定理得:$\frac{a}{sinA}$=$\frac{1}{\frac{1}{2}}$=2R=2,即R=1,
∴三角形ABC外接圆面积S=πR2=π.
故答案为:π.
点评 此题考查了正弦、余弦定理,以及圆的面积公式的应用,熟练掌握定理及公式是解本题的关键,属于基础题.

练习册系列答案
相关题目
5.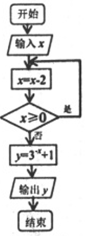 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )
 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )| A. | $\frac{4}{3}$ | B. | 10 | C. | 4 | D. | 2 |
12.已知全集U=R,集合A={x|x2>4},B={x|$\frac{x+3}{x-1}$≤0},则(∁UA)∩B等于( )
| A. | {x|-2≤x<1} | B. | {x|-3≤x<2} | C. | {x|-2≤x<2} | D. | {x|-3≤x≤2} |
9.某校高二年级共有2000人,其中男生1100人,女生900人,为调查该年级学生每周平均体育运动时间的情况,采用分成抽样的方法抽取200人进行分析,统计的数据如表(时间单位:小时).
男、女运动时间情况的调查表:
(Ⅰ)计算x,y的值,根据以上统计数据完成下面的每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该级部学生的每周平均体育运动时间与性别有关”.
附:
(Ⅱ)在每周平均体育运动时间在8小时以上的被调查的人中,喜欢乒乓球的有6人,其中男生4人,女生2人;级部决定从这4名男省中选2人,2名女生中选1人,组成代表队参加校运动会,则男生A和女生E恰好都被选中的概率是多少?
男、女运动时间情况的调查表:
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
5.春节期间和谐小区从初一至初八连续8天举办大型文艺汇演,居民甲随机选择其中的连续3天观看演出,那么他在初一至初四期间连续3天看演出的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |