题目内容
设点P(x,y)在椭圆
+
=1上移动,则x+y的最大值等于 .
| x2 |
| 9 |
| y2 |
| 4 |
考点:椭圆的参数方程,三角函数的最值
专题:坐标系和参数方程
分析:化椭圆方程为参数方程可得
,可得x+y=3cosθ+2sinθ=
sin(θ+φ),可得最值.
|
| 13 |
解答:
解:化椭圆
+
=1为参数方程
,
∴x+y=3cosθ+2sinθ=
sin(θ+φ),其中tanφ=
,
∴x+y的最大值等于
故答案为:
| x2 |
| 9 |
| y2 |
| 4 |
|
∴x+y=3cosθ+2sinθ=
| 13 |
| 3 |
| 2 |
∴x+y的最大值等于
| 13 |
故答案为:
| 13 |
点评:本题考查椭圆的参数方程,涉及三角函数的最值,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点(1,0,4)在空间直角坐标系中的位置是( )
| A、y轴上 |
| B、xOy平面上 |
| C、xOz平面上 |
| D、yOz平面上 |
若函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的取值范围是( )
| A、(-1,2) |
| B、(-∞,-3)∪(6,+∞) |
| C、(-3,6) |
| D、(-∞,-1)∪(2,+∞) |
 如图所示,四棱锥P-ABCD,底面四边形ABCD是正方形,侧面PCD是边长为a的正三角形,且平面PCD⊥底面ABCD,E为PC的中点.
如图所示,四棱锥P-ABCD,底面四边形ABCD是正方形,侧面PCD是边长为a的正三角形,且平面PCD⊥底面ABCD,E为PC的中点. 正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°
正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°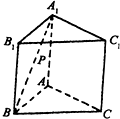 如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.