题目内容
6.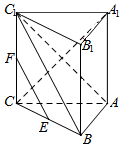 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AA1,E、F分别是棱BC、CC1的中点.(Ⅰ)若线段AC上的点D满足平面DEF∥平面ABC1,试确定点D的位置,并说明理由;
(Ⅱ)证明:EF⊥A1C.
分析 (I)利用已知及面面平行的性质可得AB∥DE,由E是棱BC的中点,即可得D是线段AC的中点.
(II)先证明A1C⊥AC1,又由(1)可得AB⊥A1C,可证A1C⊥面ABC1,即可证明A1C⊥BC1,又EF∥BC1,从而得证EF⊥A1C.
解答 (本题满分为12分) 解:(I)∵面DEF∥面ABC1,面ABC∩面DEF=DE,面ABC∩面ABC1=AB,
解:(I)∵面DEF∥面ABC1,面ABC∩面DEF=DE,面ABC∩面ABC1=AB,
∴AB∥DE,-------(4分)
∵在△ABC中E是棱BC的中点,
∴D是线段AC的中点.------------(6分)
(II)∵三棱柱ABC-A1B1C1中AC=AA1,
∴侧面A1ACC1是菱形,
∴A1C⊥AC1,--------------------------------(7分)
由(1)可得AB⊥A1C,
∵AB∩AC1=A,
∴A1C⊥面ABC1,---------------(9分)
∴A1C⊥BC1.-------(10分)
又∵E,F分别为棱BC,CC1的中点,
∴EF∥BC1,--------(11分)
∴EF⊥A1C.---------(12分)
点评 本题主要考查了面面平行的性质,直线与平面垂直的判定和性质的应用,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.设点P是椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{25}$=1上的一点,F1,F2是椭圆的两个焦点,若PF1⊥PF2,则|PF1|与|PF2|差的绝对值是( )
| A. | 0 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{15}$ |
17.设不等式组$\left\{\begin{array}{l}{2x-3y+6≥0}\\{4x-y-8≤0}\\{x+y-2≥0}\end{array}\right.$表示的平面区域为Ω,则当直线y=k(x-1)与区域Ω有公共点时,k的取值范围是( )
| A. | [-2,+∞) | B. | (-∞,0] | C. | [-2,0] | D. | (-∞,-2]∪[0,+∞) |
14.如图,在正方形ABCD中,AD=4,E为DC上一点,且$\overrightarrow{DE}$=3$\overrightarrow{EC}$,则$\overrightarrow{AB}$•$\overrightarrow{AE}$( )
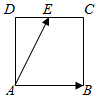

| A. | 20 | B. | 16 | C. | 15 | D. | 12 |
11.下列判断错误的是( )
| A. | 命题“若am2≤bm2,则a≤b”是假命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x0∈R,${{x}_{0}}^{3}$-${{x}_{0}}^{2}$-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 命题“p∨q为真命题”是命题“p∧q为真”的充分不必要条件 |
16.若集合M={x|x2-2x-3<0},N={x|x>1},则M∩N=( )
| A. | (1,3] | B. | (1,3) | C. | [1,3) | D. | [1,3] |