题目内容
设f（cosx-1）=cos2x，求f（x）= ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：可以令cosx-1=t，利用换元法求出f（x）的解析式；
解答：
解：∵f（cosx-1）=cos2x，设cosx-1=t，t∈[-2，0]
∴cosx=1+t，
∴cos2x=t2+2t+1，
∴f（t）=t2+2t+1，
∴f（x）=x2+2x+1，x∈[-2，0]，
故答案为：x2+2x+1，x∈[-2，0]，
∴cosx=1+t，
∴cos2x=t2+2t+1，
∴f（t）=t2+2t+1，
∴f（x）=x2+2x+1，x∈[-2，0]，
故答案为：x2+2x+1，x∈[-2，0]，
点评：本题主要考查函数解析式的求法，本题利用换元法进行求解，比较方便，此题是一道基础题；
练习册系列答案
相关题目
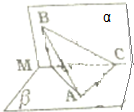在直二面角α-MN-β中，等腰直角△ABC的斜边BC?α，一直角边AC?β，BC与β所成角的正弦值为
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|