题目内容
9.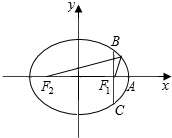 电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.
电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.
分析 设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),把x=c代入椭圆方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得y=±$\frac{{b}^{2}}{a}$.可得$\frac{2{b}^{2}}{a}$=|BC|=5.2,又|F1A|=1.5=a-c,a2=b2+c2,联立解出即可得出.
解答 解:设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
把x=c代入椭圆方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得y=±$\frac{{b}^{2}}{a}$.
∴$\frac{2{b}^{2}}{a}$=|BC|=5.2,|F1A|=1.5=a-c,又a2=b2+c2,
联立解得a=$\frac{45}{8}$,c=$\frac{33}{8}$.
∴聚光灯泡F1与影片门F2之间距离=2c=$\frac{33}{4}$cm.
答:聚光灯泡F1与影片门F2之间应该距离$\frac{33}{4}$cm.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.已知z(1-i)=2i(z为虚数单位),则z的共轭复数$\overline{z}$所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.设点A,B,C为球O的球面上三点,O为球心.球O的表面积为100π,且△ABC是边长为$4\sqrt{3}$的正三角形,则三棱锥O-ABC的体积为( )
| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点和左焦点分别为A、F,O为坐标原点,点H的坐标为H(-$\frac{{a}^{2}}{c}$,0),若$\overrightarrow{AF}$=λ$\overrightarrow{OH}$,则实数λ的值可能是( )
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.已知函数$f(x)=\frac{1}{2}cos(ω\;x+\frac{π}{3})$,且f(x+3)-f(x)=0,则ω为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
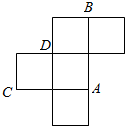 如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.