题目内容
8.在△ABC中,|$\overrightarrow{AB}+\overrightarrow{AC}$|=$\sqrt{3}$|$\overrightarrow{AB}-\overrightarrow{AC}$|,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=3,则$\overrightarrow{CB}•\overrightarrow{CA}$=( )| A. | 3 | B. | -3 | C. | $\frac{9}{2}$ | D. | -$\frac{9}{2}$ |
分析 由题意,画出图形,利用向量的平行四边形法则得到对角线长度的关系,求出OC,得到△ABC 的形状即可求得.
解答 解:由平面向量的平行四边形法则得到,在△ABC中,|$\overrightarrow{AB}+\overrightarrow{AC}$|=$\sqrt{3}$|$\overrightarrow{AB}-\overrightarrow{AC}$|,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=3,如图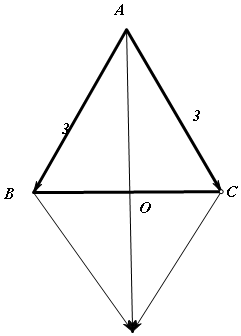 ,设|OC|=x,则|OA|=$\sqrt{3}$x,所以|AO|2+|OC|2=|AC|2即3x2+x2=9,解得x=$\frac{3}{2}$,
,设|OC|=x,则|OA|=$\sqrt{3}$x,所以|AO|2+|OC|2=|AC|2即3x2+x2=9,解得x=$\frac{3}{2}$,
所以|BC|=3,所以△ABC为等边三角形,所以$\overrightarrow{CB}•\overrightarrow{CA}$=3×3×$\frac{1}{2}$=$\frac{9}{2}$;
故选:C.
点评 本题考查向量加法的平行四边形法则,向量数量积的计算公式;关键是正确判断三角形的形状.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
17.平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{a}$+$\overrightarrow{b}$=( )
| A. | $\overrightarrow{AC}$ | B. | $\overrightarrow{CA}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DB}$ |
18.过点M(-3,2),N(-2,3)的直线倾斜角是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |



