题目内容
9.不等式(x+1)(x2-4x+3)>0有多种解法,其中有一种方法如下,在同一直角坐标系中作出y1=x+1和y2=x2-4x+3的图象然后进行求解,请类比求解以下问题:设a,b∈Z,若对任意x≤0,都有(ax+2)(x2+2b)≤0,则a+b=-1.
分析 若对任意x≤0,都有(ax+2)(x2+2b)≤0,则y1=ax+2应为增函数,y2=x2+2b的图象顶点应在x轴下方,且函数与x负半轴交于同一点,结合a,b∈Z,可得答案.
解答 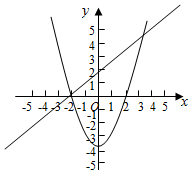 解:类比图象法解不等式的方法,在同一坐标系中,画出y1=ax+2和y2=x2+2b的图象,
解:类比图象法解不等式的方法,在同一坐标系中,画出y1=ax+2和y2=x2+2b的图象,
若对任意x≤0,都有(ax+2)(x2+2b)≤0,则两个函数图象应如下图所示:
则$\left\{\begin{array}{l}a>0\\ b<0\\-\frac{2}{a}=-\sqrt{-2b}\end{array}\right.$,
由a,b∈Z得:$\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$,
∴a+b=-1,
故答案为:-1
点评 本题考查的知识点是类比推理,数形结合思想,转化思想,难度中档.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
4.“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.若z=$\frac{3+2i}{i}$,则|$\overline{z}$-1|等于( )
| A. | 3 | B. | 5 | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
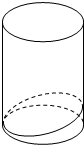 如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.
如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.