题目内容
1．函数y=$\frac{2}{x}$在区间（0，+∞）上是减函数．（填“增”或“减”）分析 由单调性的定义任取x1，x2∈（0，+∞）且x1＜x2，作出变形判断即可．
解答 解：任取x1，x2∈（0，+∞）且x1＜x2，
则$\frac{2}{{x}_{1}}$-$\frac{2}{{x}_{2}}$=$\frac{2（{x}_{2}-{x}_{1}）}{{x}_{1}{x}_{2}}$＞0，即$\frac{2}{{x}_{1}}$＞$\frac{2}{{x}_{2}}$，
∴函数y=$\frac{2}{x}$在区间（0，+∞）上是减函数，
故答案为：减
点评 本题考查函数单调性的判断与证明，属基础题．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
13．
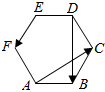如图，正六边形ABCDEF中，设$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{DB}$=$\overrightarrow{b}$，则$\overrightarrow{EF}$等于（ ）
如图，正六边形ABCDEF中，设$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{DB}$=$\overrightarrow{b}$，则$\overrightarrow{EF}$等于（ ）| A． | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B． | $\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$ | C． | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D． | $\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ |