题目内容
4．“a=3”是“直线ax+2y+3a=0与直线3x+（a-1）y=a-7相互垂直”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据直线垂直的条件，结合充分条件和必要条件的定义进行判断即可
解答 解：直线ax+2y+3a=0与直线3x+（a-1）y=a-7相互垂直，
所以3a+2（a-1）=0，
解得a=$\frac{2}{5}$
所以“a=3”是“直线ax+2y+3a=0与直线3x+（a-1）y=a-7相互垂直″的既不充分也不必要条件，
故选：D．
点评 本题通过逻辑来考查两直线垂直的判定，必要条件、充分条件与充要条件的判断，考查基本知识的应用．
练习册系列答案
相关题目
13．
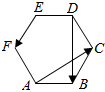如图，正六边形ABCDEF中，设$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{DB}$=$\overrightarrow{b}$，则$\overrightarrow{EF}$等于（ ）
如图，正六边形ABCDEF中，设$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{DB}$=$\overrightarrow{b}$，则$\overrightarrow{EF}$等于（ ）| A． | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B． | $\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$ | C． | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D． | $\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ |