题目内容
8.已知递增的等比数列{an}满足:a2•a3=8,a1+a4=9(1)求数列{an}的通项公式;
(2)设数列$\left\{{b_n}\right\}:{b_n}=2({2n-1}){a_n}(n∈{N^+})$,求数列{bn}的前n项的和Tn.
分析 (1)利用等比数列的性质得到a2a3=a1a4=8,又a1+a4=9,由此求得首项和公比;根据等比数列的通项公式求得an=2n-1;
(2)利用“错位相减法求和法”进行解答即可.
解答 解:(1)由题意,得a2a3=a1a4=8,又a1+a4=9,
所以a1=1,a4=8,或 a1=8,a4=1,
由{an}是递增的等比数列,知q>1所以a1=1,a4=8,且q=2,
∴${a_n}={a_1}{q^{n-1}}=1×{2^{n-1}}={2^{n-1}}$,即an=2n-1;
(2)由(1)得$b{\;}_n=2({2n-1}){a_n}=({2n-1}){2^n}$,
所以${T_n}=1•{2^1}+3•{2^2}+5•{2^3}+…+(2n-1)•{2^n}$
所以$2{T_n}=1•{2^2}+3•{2^3}+5•{2^4}+…+(2n-1)•{2^{n+1}}$,
两式相减,得
$-{T_n}=1•{2^1}+2({2^2}+{2^3}+…+{2^n})-(2n-1){2^{n+1}}$,
得${T_n}=({2n-3})•{2^{n+1}}+6$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法求和法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
18.若命题p:?x∈A,2x∈B,则( )
| A. | ¬p:?x0∈A,2x0∈B | B. | ¬p:?x0∉A,2x0∈B | C. | ¬p:?x0∈A,2x0∉B | D. | ¬p:?x∉A,2x∉B |
13.下列函数中既是偶函数,又在(0,+∞)上单调递减的为( )
| A. | $y={x^{-\frac{1}{2}}}$ | B. | y=x-2 | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x2 |
17.程序框图如图所示,当$A=\frac{12}{13}$时,输出的k的值为( )


| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
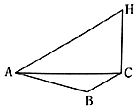 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.