题目内容
已知|
|=1,|
|=
,
•
=0,点C在∠AOB内,且C(
,
),设
=m
+n
(m,n∈R),则
的值为( )
| OA |
| OB |
| 3 |
| OA |
| OB |
| 3 |
| 4 |
| ||
| 4 |
| OC |
| OA |
| OB |
| m |
| n |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
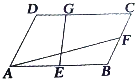
分析:如图所示,A(1,0),B(0,
).由
=m
+n
,可得(
,
)=m(1,0)+n(0,
).解出即可.
| 3 |
| OC |
| OA |
| OB |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
解答:
解:如图所示,
A(1,0),B(0,
).
∵
=m
+n
,
∴(
,
)=m(1,0)+n(0,
).
∴m=
,
n=
,解得n=
.
∴
=3.
故选:B.

A(1,0),B(0,
| 3 |
∵
| OC |
| OA |
| OB |
∴(
| 3 |
| 4 |
| ||
| 4 |
| 3 |
∴m=
| 3 |
| 4 |
| 3 |
| ||
| 4 |
| 1 |
| 4 |
∴
| m |
| n |
故选:B.
点评:本题考查了向量线性运算、向量基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2sin15°cos15°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设复数z满足z(1+i)=2(i为虚数单位),则z=( )
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
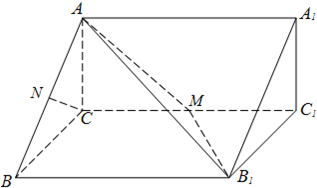 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.