题目内容
已知数列{an}中,a3=2,a7=1,且数列{
}为等差数列,则a5= .
| 1 |
| an+1 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:根据等差数列的性质建立条件关系,即可得到结论.
解答:
解:若数列{
}为等差数列,设bn=
,
则b3=
=
=
,b7=
=
,则b5=
,
则2b5=b3+b7=
+
=
,
即b5=
=
,
解得a5=
,
故答案为:
| 1 |
| an+1 |
| 1 |
| an+1 |
则b3=
| 1 |
| a3+1 |
| 1 |
| 2+1 |
| 1 |
| 3 |
| 1 |
| a7+1 |
| 1 |
| 2 |
| 1 |
| a5+1 |
则2b5=b3+b7=
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
即b5=
| 1 |
| a5+1 |
| 5 |
| 12 |
解得a5=
| 7 |
| 5 |
故答案为:
| 7 |
| 5 |
点评:本题主要考查等差数列性质的应用,构造新的等差数列是解决本题的关键.

练习册系列答案
相关题目
已知p:
≤x≤1,q:x2-(a+1)x+a≤0,若a<
,则p是q的( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
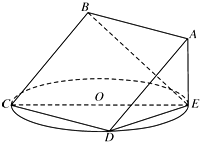 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点. 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是