题目内容
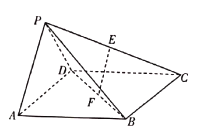
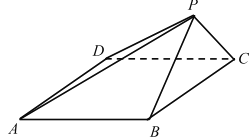
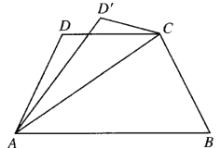
【题目】如图,已知四边形![]() 是底角为
是底角为![]() 的等腰梯形,且
的等腰梯形,且![]() ,沿直线
,沿直线![]() 将
将![]() 翻折成
翻折成![]() ,所成二面角
,所成二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
作出图形,设![]() ,作出二面角
,作出二面角![]() 的平面角,由余弦定理求出
的平面角,由余弦定理求出![]() 、
、![]() 、
、![]() 的余弦值,结合余弦函数的单调性可得出
的余弦值,结合余弦函数的单调性可得出![]() 、
、![]() 、
、![]() 的大小关系.
的大小关系.
设![]() 的中点为点
的中点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,在底面
,在底面![]() 内,过点
内,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,
,

设![]() ,由四边形
,由四边形![]() 为底角为
为底角为![]() 的等腰梯形,且
的等腰梯形,且![]() ,可得
,可得![]() ,
,![]() ,
,
![]() ,
,![]() 为
为![]() 的中点,则
的中点,则![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为菱形,
为菱形,
所以,![]() 为线段
为线段![]() 的垂直平分线,
的垂直平分线,
则![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
在翻折的过程中,点![]() 在底面
在底面![]() 内的投影在线段
内的投影在线段![]() 上,
上,
所以,![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
当点![]() 在底面
在底面![]() 内的投影在线段
内的投影在线段![]() 上时,
上时,![]() ,
,
而![]() ,所以此时
,所以此时![]() ;
;
当点![]() 在底面
在底面![]() 内的投影在线段
内的投影在线段![]() 上时,则
上时,则![]() ,
,![]() ,
,![]() ,
,
则在![]() 中,由余弦定理得
中,由余弦定理得 ,
,
在![]() 中,由余弦定理得
中,由余弦定理得 ,
,
则![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以此时![]() .
.
综上所述,![]() .
.
故选:B.

【题目】已知A,B是抛物线![]() 上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
(1)求证:直线PQ平行于x轴;
(2)若直线AB经过抛物线T的焦点,求![]() 面积的最小值.
面积的最小值.
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为![]() 万元/辆和
万元/辆和![]() 万元/辆的
万元/辆的![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)从![]() 和
和![]() 的车型中各随机抽取
的车型中各随机抽取![]() 车,以
车,以![]() 表示这
表示这![]() 车中使用寿命不低于
车中使用寿命不低于![]() 年的车数,求
年的车数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租车每年上交公司![]() 万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这
万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这![]() 辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
附: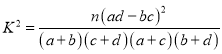 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |