题目内容
【题目】个人所得税是国家对本国公民、居住在本国境内的个人的所得和境外个人来源于本国的所得征收的一种所得税.我国在1980年9月10日,第五届全国人民代表大会第三次会议通过并公布了《中华人民共和国个人所得税法》.公民依法诚信纳税是义务,更是责任现将自2013年至2017年的个人所得税收入统计如下

并制作了时间代号x与个人所得税收入的如如图所示的散点图:
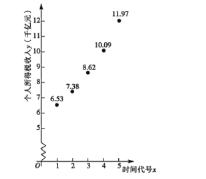
根据散点图判断,可用①y=menx与②![]() 作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:
作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:

以下计算过程中四舍五入保留两位小数.
(1)根据所给数据,分别求出①,②中y关于x的回归方程;
(2)已知2018年个人所得税收人为13.87千亿元,用2018年的数据验证(1)中所得两个回归方程,哪个更适宜作为y关于时间代号x的回归方程?
(3)你还能从统计学哪些角度来进一步确认哪个回归方程更适宜? (只需叙述,不必计算)
附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: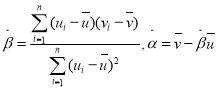
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)①y=menx,两边取对数得:![]() ,令
,令![]() ,转化为线性回归分析,利用表中数据,代入
,转化为线性回归分析,利用表中数据,代入 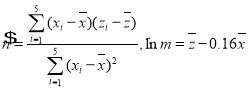 求解.②
求解.②![]() ,令
,令![]() ,转化为性回归分析,利用表中数据,代入
,转化为性回归分析,利用表中数据,代入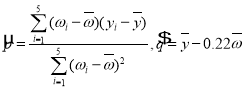 求解.
求解.
(2)将![]() ,分别代入
,分别代入![]() ,
,![]() 求值比较,哪个更接接近13.87千亿元,哪个就适宜作为y关于时间代号x的回归方程.
求值比较,哪个更接接近13.87千亿元,哪个就适宜作为y关于时间代号x的回归方程.
(3)还可以计算两个回归方程的残差,残差的平方和越小,拟合效果越好.
(1)①因为y=menx,
两边取对数得:![]() ,
,
令![]() ,
,
由表中数据得:![]() ,
,
所以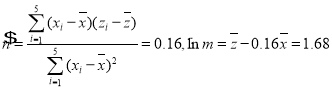 ,
,
所以![]() ,
,
所以![]() ,
,
②![]() ,
,
令![]() ,
,
![]() ,
,
由表中数据得:![]() ,
,
所以 ,
,
所以![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,
因为2018年个人所得税收人为13.87千亿元,
所以![]() 更适宜作为y关于时间代号x的回归方程.
更适宜作为y关于时间代号x的回归方程.
(3)还可以计算两个回归方程的残差,残差的平方和越小,拟合效果越好.