题目内容
【题目】下列关于函数![]() 的叙述正确的为( )
的叙述正确的为( )
A.函数![]() 有三个零点
有三个零点
B.点(1,0)是函数![]() 图象的对称中心
图象的对称中心
C.函数![]() 的极大值点为
的极大值点为![]()
D.存在实数a,使得函数![]() 为增函数
为增函数
【答案】ABC
【解析】
令函数等于零即可求出零点个数,可判断出选项A;由![]() 可得出函数图像关于点(1,0)中心对称,可判断出选项B;由导函数求出函数单调区间,根据函数单调性即可得出最大值点,可判断出选项C;根据导函数判断出是否存在实数a,使得
可得出函数图像关于点(1,0)中心对称,可判断出选项B;由导函数求出函数单调区间,根据函数单调性即可得出最大值点,可判断出选项C;根据导函数判断出是否存在实数a,使得![]() ,可判断出选项D.
,可判断出选项D.
![]() ,令
,令![]() ,则
,则![]() 或
或![]() 或
或![]() ,
,
所以函数![]() 有三个零点,所以A正确;
有三个零点,所以A正确;
![]() ,
,
![]() ,
,
所以![]() ,所以函数
,所以函数![]() 图像关于点(1,0)对称中心,
图像关于点(1,0)对称中心,
所以B正确;求出![]() 的导函数
的导函数![]() ,
,
令![]() ,则
,则![]() 或
或![]() ,
,
令![]() ,则
,则![]() ,
,
所以函数![]() 在
在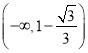 和
和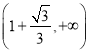 上单调递增,
上单调递增,
在 上单调递减,所以当
上单调递减,所以当![]() 时
时
函数![]() 有极大值,所以函数
有极大值,所以函数![]() 的极大值点为
的极大值点为![]() ,
,
所以C正确;假设函数![]() 为增函数,
为增函数,
则![]() 恒成立,由上可知当
恒成立,由上可知当![]() 或
或![]() 时,
时,
![]() ,若要满足
,若要满足![]() ,则需在
,则需在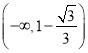 和
和
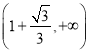 上
上![]() 恒成立,
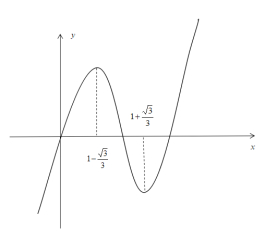
恒成立,![]() 图像如下,
图像如下,
如图所示函数![]() 在
在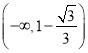 上不可能恒成立,所以不存在这样的实数a,所以D错误.
上不可能恒成立,所以不存在这样的实数a,所以D错误.
故选:ABC

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目