题目内容
6.已知$\vec a$与$\vec b$为非零向量,$|\vec a+\vec b|=|\vec a-\vec b|$,且$(\vec a+\vec b)⊥(\vec a-\vec b)$,则$(\vec a+\vec b)$与$\vec b$的夹角为45°.分析 根据向量的夹角公式,以及向量的垂直,向量模计算即可.
解答 解:设$(\vec a+\vec b)$与$\vec b$的夹角为θ,
∵$|\vec a+\vec b|=|\vec a-\vec b|$,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$-$\overrightarrow{b}$|2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∵$(\vec a+\vec b)⊥(\vec a-\vec b)$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,
∴$|\overrightarrow{a}|$=$|\overrightarrow{b}|$,
∴$(\vec a+\vec b)$•$\vec b$=${\overrightarrow{b}}^{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{b}$|,
∴cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{b}|}$=$\frac{\sqrt{2}}{2}$,
∵0≤θ≤180°,
∴θ=45°,
故答案为:45°.
点评 本题考查了向量的数量积的运算以及向量的模的计算以及向量垂直的条件,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
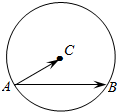 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.