题目内容
13．命题“?x∈R，x2-5x+1＞0”的否定为（ ）| A． | ?x∈R，x2-5x+1≤0 | B． | ?x∈R，x2-5x+1≤0 | C． | ?x∈R，x2-5x+1＜0 | D． | ?x∈R，x2-5x+1＞0 |
分析 直接写出全程命题的否定得答案．
解答 解：命题“?x∈R，x2-5x+1＞0”的否定为：?x∈R，x2-5x+1≤0．
故选：B．
点评 本题考查全程命题的否定，关键是掌握格式，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
3．下列正确的是（ ）
| A． | 如果两个复数的积是实数，那么这两个复数互为共轭复数 | |
| B． | 用反证法证明命题“设a，b为实数，则方程x2+ax+b=0至少有一个实根”时，要做的假设是：方程x2+ax+b=0至多有一个实根 | |
| C． | 观察下列各式：a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…则可得到a10+b10=122 | |
| D． | 在复平面中复数z满足|z|=2的点的轨迹是以原点为圆心，以2为半径的圆 |
4．已知命题p：?x∈R，x2-x-2≥0，那么命题?p为（ ）
| A． | ?x∈R，x2-x-2≤0 | B． | ?x∈R，x2-x-2＜0 | C． | ?x∈R，x2-x-2≤0 | D． | ?x∈R，x2-x-2＜0 |
8．
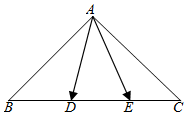如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）
如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）| A． | $[{\frac{8}{9}，\;\frac{4}{3}}]$ | B． | $[{\frac{4}{3}，\;\frac{8}{3}}]$ | C． | $[{\frac{8}{9}，\;\frac{8}{3}}]$ | D． | $[{\frac{4}{3}，\;+∞}）$ |
5．
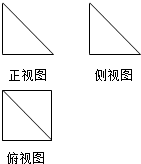一个几何体的三视图如图所示，其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形，则该几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |