题目内容
在△ABC中，b=8，c=3，A=60°，则此三角形的外接圆的面积为 ．
考点：正弦定理
专题：解三角形
分析：利用余弦定理列出关系式，把b，c，cosA的值代入求出a的值，再利用正弦定理求出三角形外接圆半径，即可确定出外接圆面积．
解答：
解：∵在△ABC中，b=8，c=3，A=60°，
∴由余弦定理得：a2=b2+c2-2bccosA=64+9-24=49，即a=7，
由正弦定理得：
=2R，即R=
=
=
，
则此三角形外接圆面积为
π，
故答案为：
π
∴由余弦定理得：a2=b2+c2-2bccosA=64+9-24=49，即a=7，
由正弦定理得：
| a |
| sinA |
| a |
| 2sinA |
| 7 | ||||
2×
|
7
| ||
| 3 |
则此三角形外接圆面积为
| 49 |
| 3 |
故答案为：
| 49 |
| 3 |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
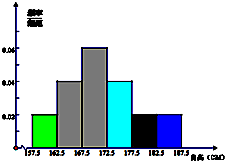云南省2014年全省高中男生身高统计调查数据显示：全省100000名男生的平均身高为170.5cm．现从我校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于157.5cm和187.5cm之间，将测量结果按如下方式分成6组：第一组[157.5，162.5]，第二组[162.5，167.5]，…，第6组[182.5，187.5]，设f（x）=x+ln（x+
），若对于任意的实数a和b，都有f（a）+f（b）＞0，则必有（ ）
| 1+x2 |
| A、a+b＞0 |
| B、a-b＞0 |
| C、a+b＜0 |
| D、a-b＜0 |
（2012•安徽）（log29）•（log34）等于（ ）
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|