题目内容
已知p:M∈{(x,y)||x|+|x-2|+
≤3};q:M∈{(x,y)|(x-1)2+y2<r2}(r>0).如果p是q的充分但不必要条件,则r的取值范围是 .
| y2+2y+2 |
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆,简易逻辑
分析:化简命题p,结合充分条件和必要条件的定义以及利用数形结合即可得到结论.
解答:
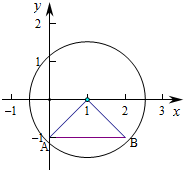 解:∵
解:∵
=
≥1,|x|+|x-2|≥2,
∴|x|+|x-2|+
≥3,
∴若|x|+|x-2|+
≤3则等价为|x|+|x-2|+
=3;
此时y=-1,0≤x≤2
即M∈{(x,y)|y=-1,0≤x≤2};
作出M对应的区域如图,
若p是q的充分但不必要条件,
则线段AB在圆的内部,
则满足圆心到A和B的距离小于半径即可,
即
<r,
即r>
,
故答案为:r>
.
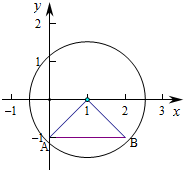 解:∵
解:∵| y2+2y+2 |
| (y+1)2+1 |
∴|x|+|x-2|+
| y2+2y+2 |
∴若|x|+|x-2|+
| y2+2y+2 |
| y2+2y+2 |
此时y=-1,0≤x≤2
即M∈{(x,y)|y=-1,0≤x≤2};
作出M对应的区域如图,
若p是q的充分但不必要条件,
则线段AB在圆的内部,
则满足圆心到A和B的距离小于半径即可,
即
| 12+12 |
即r>
| 2 |
故答案为:r>
| 2 |
点评:本题主要考查充分条件和必要条件的应用,化简命题p是解决本题的关键.综合性较强.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
在区间(0,+∞)上是减函数的是( )
| A、y=2x | ||
B、y=log
| ||
| C、y=2x | ||
| D、y=x2 |
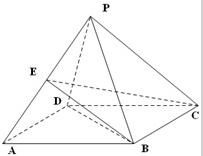 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=