题目内容
20．如图，在正六边形ABCDEF中，|$\overrightarrow{AC}$+$\overrightarrow{AE}$|=6，则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于（ ）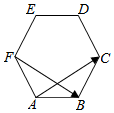
| A． | -6 | B． | 6 | C． | -2$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
分析 由题意可知，△ACE为等边三角形，继而求出三角形的高，再根据向量的数量积公式即可求出．
解答 解：在正六边形ABCDEF中，
∵AB=DC，
∴△ACE为等边三角形，
∵|$\overrightarrow{AC}$+$\overrightarrow{AE}$|=6，
∴△ACE为的高为3，
∴AC=2$\sqrt{3}$，
∴AB=2，
∴$\overrightarrow{AF}$•$\overrightarrow{FB}$=2×2$\sqrt{3}$cos（180°-30°）=-6，
故答案为：-6．
点评 本题考查了等边三角形的知识和向量的模以及向量的数量积公式，属于中档题．
练习册系列答案
相关题目
如图，圆柱O-O1中，AB为下底面圆O的直径，CD为上底面圆O1的直径，AB∥CD，点 E、F在圆O上，且AB∥EF，且AB=2，AD=1．
5．已知集合M={x|-x≤x＜3}，集合N={x|y=$\sqrt{-{x}^{2}-x+6}$}，则M∪N=（ ）
| A． | M | B． | N | C． | {x|-1≤x≤2} | D． | {x|-3≤x＜3} |
9．若m，n表示不同直线，α，β表示不同的平面，则下列结论中正确的是（ ）
| A． | 若m∥α，m∥n，则n∥α | B． | 若m?α，n?β，m∥β，n∥α，则α∥β | ||
| C． | 若α⊥β，m∥α，n∥β，则m∥n | D． | 若α∥β，m∥α，n∥m，n?β，则n∥β |