题目内容
11.已知Sn是数列{an}的前n项和,且满足2Sn=3an-3(n∈N+),等差数列{bn}的前n项和为Tn,且b5+b13=34,T3=9.(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)若数列{cn}的通项公式为cn=anbn,问是否存在互不相等的正整数m,k,r使得m,k,r成等差数列,且cm,ck,cr成等比数列?若存在,求出m,k,r;若不存在,说明理由.
分析 (Ⅰ)根据等差数列的前n项和公式和数列的递推公式,即可求出答案,
(Ⅱ)由(Ⅰ)可知Cn=(2n-1)•3n,假设存在互不相等且大于2的正整数m,k,r满足条件,得出矛盾即可.
解答 解:(Ⅰ)由2Sn=3an-3(n∈N+)令n=1可知a1=3,
当n≥2时,有2Sn-1=3an-1-3,两式相减得2an=3an-3an-1,
∴an=3an-1(n≥2),
∴数列{an}是以3为首项,3为公比的等比数列,
∴${a_n}={3^n}$.
设等差数列{bn}的公差为d,依题意得,$\left\{{\begin{array}{l}{2{b_1}+16d=34}\\{3{b_1}+3d=9}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{{b_1}=1}\\{d=2}\end{array}}\right.$,
∴bn=2n-1;
(Ⅱ)由(1)可知${c_n}={a_n}{b_n}=(2n-1){3^n}$,
假设存在互不相等的正整数m,k,r,使得m,k,r成等差数列,且cm,ck,cr成等比数列.则${c_k}^2={c_m}{c_r}$,
即(2k-1)2•32k=(2m-1)(2r-1)•3m+r.(*),
由m,k,r成等差数列,得2k=m+r,所以32k=3m+r.
所以由(*)得(2k-1)2=(2m-1)(2r-1).即4k2-4k+1=4mr-2(m+r)+1,
又2k=m+r,所以k2=mr,即${(\frac{m+r}{2})^2}=mr$,即(m-r)2=0即m=r.这与m≠r矛盾,
所以,不存在满足条件的正整数m,k,r,使得m,k,r成等差数列,且cm,ck,cr成等比数列.
点评 本题是一道关于数列递推式的综合题,考查分析问题、解决问题的能力,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 相交 | B. | 相离 | C. | 相切 | D. | 与θ的取值有关 |
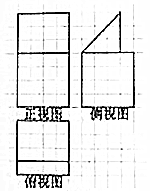
| A. | 93+12$\sqrt{2}$ | B. | 97+12$\sqrt{2}$ | C. | 105+12$\sqrt{2}$ | D. | 109+12$\sqrt{2}$ |
| A. | $-\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{π}{3}$ |
 某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )
某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )| A. | 48 | B. | 54 | C. | 60 | D. | 64 |
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.