题目内容
设a为实数,函数f(x)=2x2+(x-a)|x-a|
(Ⅰ)若f(0)≥1,求a的取值范围;
(Ⅱ)求f(x)在[-2,2]上的最小值.
(Ⅰ)若f(0)≥1,求a的取值范围;
(Ⅱ)求f(x)在[-2,2]上的最小值.
考点:分段函数的应用,函数的值域
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)原不等式即为-a|a|≥1,考虑a<0,解二次不等式求交集即可;
(Ⅱ)将函数f(x)改写为分段函数,讨论当a≥0时,①-a≤-2,②-a>-2,当a<0时,①
≤-2,②
>-2,运用二次函数的单调性,即可得到最小值.
(Ⅱ)将函数f(x)改写为分段函数,讨论当a≥0时,①-a≤-2,②-a>-2,当a<0时,①
| a |
| 3 |
| a |
| 3 |
解答:
解:(Ⅰ) 若f(0)≥1,则-a|a|≥1⇒
⇒a≤-1,
则a的取值范围是(-∞,-1];
(Ⅱ)函数f(x)=2x2+(x-a)|x-a|=
,
当a≥0时,
①-a≤-2即a≥2时,f(x)在[-2,2]上单调递增,所以
f(x)min=f(-2)=4-4a-a2;
②-a>-2即0≤a<2时,f(x)在[-2,-a]上单调递减,在[-a,2]上单调递增,所以
f(x)min=f(-a)=-2a2;
当a<0时,
①
≤-2即a≤-6时,f(x)在[-2,2]上单调递增,所以
f(x)min=f(-2)=12+4a+a2;
②
>-2即-6<a<0时,f(x)在[-2,
]上单调递减,在[
,2]上单调递增,所以
f(x)min=f(
)=
,
综上可得,f(x)min=
|
则a的取值范围是(-∞,-1];
(Ⅱ)函数f(x)=2x2+(x-a)|x-a|=
|
当a≥0时,
①-a≤-2即a≥2时,f(x)在[-2,2]上单调递增,所以
f(x)min=f(-2)=4-4a-a2;
②-a>-2即0≤a<2时,f(x)在[-2,-a]上单调递减,在[-a,2]上单调递增,所以
f(x)min=f(-a)=-2a2;
当a<0时,
①
| a |
| 3 |
f(x)min=f(-2)=12+4a+a2;
②
| a |
| 3 |
| a |
| 3 |
| a |
| 3 |
f(x)min=f(
| a |
| 3 |
| 2a2 |
| 3 |
综上可得,f(x)min=
|
点评:本题考查绝对值函数的运用,考查分类讨论的思想方法,考查二次函数在闭区间上的最值,考查运算能力,属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知互不相同的直线l,m,n与平面α,β,则下列叙述错误的是( )
| A、若m∥l,n∥l,则m∥n |
| B、若m∥α,n∥α,则m∥n |
| C、若m⊥α,n∥β,则α⊥β |
| D、若m⊥β,α⊥β,则m∥α或m?α |
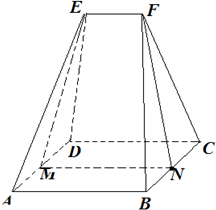 如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6 工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为50cm,内圆半径为20cm.则制作这样一面扇面需要的布料为
工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为50cm,内圆半径为20cm.则制作这样一面扇面需要的布料为