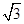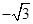题目内容
已知数列{ an }满足a1=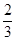 ,且对任意的正整数m,n,都有am+n= am + an,则
,且对任意的正整数m,n,都有am+n= am + an,则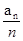 等于( )
等于( )
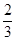 ,且对任意的正整数m,n,都有am+n= am + an,则
,且对任意的正整数m,n,都有am+n= am + an,则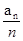 等于( )
等于( )A. | B.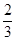 | C. | D.2 |
B
试题分析:解:∵数列{an}满足a1=
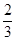 ,且对任意的正整数m,n,都有am+n=am+an,∴an=an-1+a1=an-1+
,且对任意的正整数m,n,都有am+n=am+an,∴an=an-1+a1=an-1+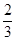 ,∴数列{an}是首项为a1=
,∴数列{an}是首项为a1=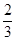 ,公差d=
,公差d=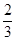 的等差数列,∴an=
的等差数列,∴an=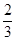 +
+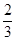 (n-1)=
(n-1)=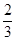 n,∴
n,∴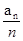 =
=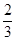 .故选B
.故选B点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的合理运用

练习册系列答案
相关题目
 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于 .
等于 . ,则常数k的值为( )
,则常数k的值为( ) 中,
中,  ,
, (
( ).
). ,
,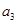 ,
, ;
; 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.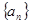 的前
的前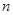 项和为
项和为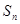 ,且满足
,且满足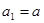 (
(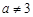 ),
),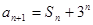 ,设
,设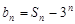 ,
,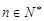 .
.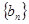 是等比数列;
是等比数列;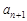 ≥
≥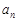 ,
,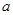 的最小值;
的最小值;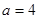 时,给出一个新数列
时,给出一个新数列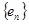 ,其中
,其中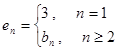 ,设这个新数列的前
,设这个新数列的前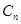 ,若
,若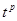 (
(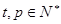 且
且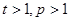 )的形式,则称
)的形式,则称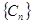 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由. 的“分裂”中最小的数为a,而
的“分裂”中最小的数为a,而 的“分裂”中最大的数是b,则a+b= .
的“分裂”中最大的数是b,则a+b= .
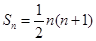
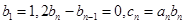 ,求数列{Cn}的前n项和Tn
,求数列{Cn}的前n项和Tn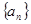 中,
中,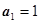 ,前
,前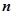 项的和为
项的和为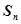 ,对任意的
,对任意的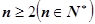 ,
,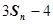 ,
,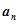 ,
,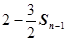 总成等差数列.
总成等差数列.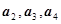 的值并猜想数列
的值并猜想数列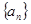 的通项公式
的通项公式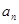
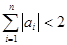 .
.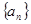 为等差数列,
为等差数列,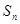 是其前n项的和,且
是其前n项的和,且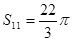 ,则
,则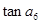 =( )
=( )