题目内容
对于大于1的自然数m的n次幂可用奇数进行如图所示的“分裂”,仿此,记 的“分裂”中最小的数为a,而
的“分裂”中最小的数为a,而 的“分裂”中最大的数是b,则a+b= .
的“分裂”中最大的数是b,则a+b= .
 的“分裂”中最小的数为a,而
的“分裂”中最小的数为a,而 的“分裂”中最大的数是b,则a+b= .
的“分裂”中最大的数是b,则a+b= .
42
试题分析:根据所给的数据,不难发现:在n
 中所分解的最大的数是2n-1;在n
中所分解的最大的数是2n-1;在n 中,所分解的最小数是n2-n+1.根据发现的规律,则6
中,所分解的最小数是n2-n+1.根据发现的规律,则6 中,最大数是6×2-1=11;6
中,最大数是6×2-1=11;6 的“分裂”中最小数是31,最后求a+b.解:6
的“分裂”中最小数是31,最后求a+b.解:6 =1+3+5+7+9+11,6
=1+3+5+7+9+11,6 =21+23+25+27+29+31, 6
=21+23+25+27+29+31, 6 中,最大数是6×2-1=11; 6
中,最大数是6×2-1=11; 6 的“分裂”中最小数是31,则则a=31,b=11.∴a+b=42,故答案为:42
的“分裂”中最小数是31,则则a=31,b=11.∴a+b=42,故答案为:42点评:此题首先要根据所提供的数据具体发现规律,然后根据发现的规律求解.规律为:在n2中所分解的最大的数是2n-1;在n3中,所分解的最小数是n2-n+1.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 的首项
的首项 ,且
,且 ,则
,则 为( )
为( ) 满足
满足 ,
, ,
, ,则
,则 的值为 .
的值为 . 是由
是由 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”. 

 的所有可能值;
的所有可能值;
 中,若
中,若 ,则
,则 等于( )
等于( ) 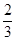 ,且对任意的正整数m,n,都有am+n= am + an,则
,且对任意的正整数m,n,都有am+n= am + an,则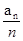 等于( )
等于( )

 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
.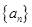 是等差数列,且满足:
是等差数列,且满足: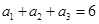 ,
,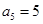 ;数列
;数列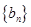 满足
满足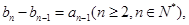
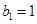 .
.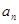 和
和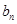 ;
;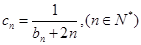 ,若
,若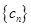 的前
的前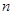 项和为
项和为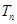 ,求证
,求证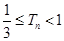 .
. 中,
中, ,且
,且 、
、 、
、 成等比数列,则数列
成等比数列,则数列