题目内容
已知数列:
,
,
,
,
,
,
,
,
,
,…,依它的前10项的规律,这个数列的第2014项a2014= .
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
考点:数列的概念及简单表示法
专题:归纳法,点列、递归数列与数学归纳法
分析:观察数列的特征,得出它的项数是1+2+3+…+k=
(k∈N*),
在每一个k段内是
,
,
,…,
,
,
(k∈N*,k≥3);
从而求出第2014项.
| k(k+1) |
| 2 |
在每一个k段内是
| k |
| 1 |
| k-1 |
| 2 |
| k-2 |
| 3 |
| 2 |
| k-2 |
| 1 |
| k-1 |
| 1 |
| k |
从而求出第2014项.
解答:
解:观察数列:
,
,
,
,
,
,
,
,
,
,…,得出:
它的项数是1+2+3+…+k=
(k∈N*),
并且在每一个k段内,是
,
,
,…,
,
,
(k∈N*,k≥3);
令
≥2014(k∈N*),
得
=2016;
又第n组是由分子、分母之和为n+1知:
2014项位于倒数第3个数,
∴该数列的第2014项为a2014=
.
故答案为:
.
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
它的项数是1+2+3+…+k=
| k(k+1) |
| 2 |
并且在每一个k段内,是
| k |
| 1 |
| k-1 |
| 2 |
| k-2 |
| 3 |
| 2 |
| k-2 |
| 1 |
| k-1 |
| 1 |
| k |
令
| k(k+1) |
| 2 |
得
| 63×64 |
| 2 |
又第n组是由分子、分母之和为n+1知:
2014项位于倒数第3个数,
∴该数列的第2014项为a2014=
| 3 |
| 61 |
故答案为:
| 3 |
| 61 |
点评:本题考查了数列的应用问题,解题时应根据数列的特征,总结出规律,才能得出正确的结论.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
先后抛掷两枚均匀的正方体骰子,骰子朝上的面的点数分别为x,y.则x,y满足方程2[log36(x+y)]2-log36(x+y)3+1=0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
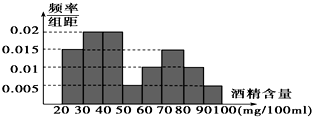 据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.
据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.