题目内容
函数f(x)=m+logax(a>0且a≠1)的图象过点(8,2)和(1,-1).
(1)求函数f(x)的解析式;
(2)令g(x)=2f(x)-f(x-1),求g(x)的最小值及取得最小值时x的值.
 解得m=-1,a=2,
解得m=-1,a=2,
故函数解析式为f(x)=-1+log2x.
(2)g(x)=2f(x)-f(x-1)
=2(-1+log2x)-[-1+log2(x-1)]
 当且仅当x-1=
当且仅当x-1= ,即x=2时,等号成立.而函数y=log2x在(0,+∞)上单调递增,则log2
,即x=2时,等号成立.而函数y=log2x在(0,+∞)上单调递增,则log2 -1≥log24-1=1,
-1≥log24-1=1,
故当x=2时,函数g(x)取得最小值1.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 ,则m的取值范围是( )
,则m的取值范围是( ) B.
B. 


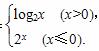 若f(a)=
若f(a)=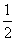 ,则实数a=( )
,则实数a=( )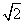
 则函数f(x)=sgn(lnx)-ln2x的零点个数为( )
则函数f(x)=sgn(lnx)-ln2x的零点个数为( )