题目内容
设全集是实数集R，A={x|-1＜x＜2}，B={x|x-a≥0}，且A⊆（∁RB），则实数a的取值范围为（ ）
| A、{a|a＜-1} |
| B、{a|a≤-1} |
| C、{a|a≥2} |
| D、{a|a＞2} |
考点：补集及其运算
专题：集合
分析：求出B中不等式的解集确定出B，进而表示出B的补集，由A为B补集的子集，求出a的范围即可．
解答：
解：由B中不等式解得：x≥a，即B={x|x≥a}，
∵全集为R，
∴∁RB={x|x＜a}，
∵A={x|-1＜x＜2}，且A⊆（∁RB），
∴a的范围为{a|a≥2}，
故选：C．
∵全集为R，
∴∁RB={x|x＜a}，
∵A={x|-1＜x＜2}，且A⊆（∁RB），
∴a的范围为{a|a≥2}，
故选：C．
点评：此题考查了补集及其运算，熟练掌握补集的定义是解本题的关键．
练习册系列答案
相关题目
已知tana=2，那么
的值为（ ）
| sina-cosa |
| 3sina+5cosa |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
sin15°cos15°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
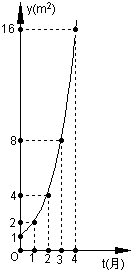如图是某池塘中的浮萍蔓延的面积y（m2）与时间t（月）的关系：y=at的图象，有以下叙述，其中正确的是（ ）