题目内容
叙述抛物线的定义,并推导抛物线的一个标准方程.
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据抛物线的定义可得结论,再建立坐标系,即可求得抛物线的一个标准方程.
解答:
 解:(1)定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
解:(1)定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
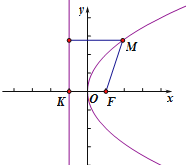
(2)过点F作直线l的垂线,垂足为K.以线段FK的重点O为坐标原点,以直线FK为x轴建立平面直角坐标系,如图.
设|FK|=p(p>0),则焦点F的坐标为(
,0),准线l的方程为x=-
.
设M(x,y)是抛物线上任意一点,点M到l的距离为d.
则|MF|=d.即
=|x+
|
化简得:y2=2px(p>0)
所以,所求标准方程为y2=2px(p>0)
 解:(1)定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.
解:(1)定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫做抛物线.这个定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.(2)过点F作直线l的垂线,垂足为K.以线段FK的重点O为坐标原点,以直线FK为x轴建立平面直角坐标系,如图.
设|FK|=p(p>0),则焦点F的坐标为(
| p |
| 2 |
| p |
| 2 |
设M(x,y)是抛物线上任意一点,点M到l的距离为d.
则|MF|=d.即
(x-
|
| p |
| 2 |
化简得:y2=2px(p>0)
所以,所求标准方程为y2=2px(p>0)
点评:本题考查抛物线的一个标准方程,考查抛物线的定义,比较基础.

练习册系列答案
相关题目
设全集是实数集R,A={x|-1<x<2},B={x|x-a≥0},且A⊆(∁RB),则实数a的取值范围为( )
| A、{a|a<-1} |
| B、{a|a≤-1} |
| C、{a|a≥2} |
| D、{a|a>2} |