题目内容
甲、乙、丙三人参加某项测试，他们能达标的概率分别是
，
，m，且三人能否达标互不影响．
（Ⅰ）若三人中至少有一人达标的概率是
，求m的值；
（Ⅱ）设甲在3次相互独立的测试中能达标的次数为随机变量ξ，求ξ的概率分布列及数学期望．
| 3 |
| 4 |
| 3 |
| 5 |
（Ⅰ）若三人中至少有一人达标的概率是
| 24 |
| 25 |
（Ⅱ）设甲在3次相互独立的测试中能达标的次数为随机变量ξ，求ξ的概率分布列及数学期望．
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：（Ⅰ）设三人中到少有一人达棱为事件A，则1-P（
）=1-（1-
）（1-
）（1-m）=
，由此能求出m．
（Ⅱ）由题意知ξ的所有可能ξ 值为0，1，2，3，分别求出相对应的概率，由此能求出ξ的分布列和Eξ．
. |
| A |
| 3 |
| 4 |
| 3 |
| 5 |
| 24 |
| 25 |
（Ⅱ）由题意知ξ的所有可能ξ 值为0，1，2，3，分别求出相对应的概率，由此能求出ξ的分布列和Eξ．
解答：
解：（Ⅰ）设三人中到少有一人达棱为事件A，
则1-P（
）=1-（1-
）（1-
）（1-m）=
，
解得m=
．
（Ⅱ）由题意知ξ的所有可能ξ 值为0，1，2，3，
P（ξ=0）=
(
)3=
，
P（ξ=1）=
(
)(
)2=
，
P（ξ=2）=
(
)2(
)=
，
P（ξ=3）=
(
)3=
∴ξ的分布列为：
Eξ=0×
+1×
+2×
+3×
=
．
则1-P（
. |
| A |
| 3 |
| 4 |
| 3 |
| 5 |
| 24 |
| 25 |
解得m=
| 3 |
| 5 |
（Ⅱ）由题意知ξ的所有可能ξ 值为0，1，2，3，
P（ξ=0）=
| C | 0 3 |
| 1 |
| 4 |
| 1 |
| 64 |
P（ξ=1）=
| C | 1 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
P（ξ=2）=
| C | 2 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 27 |
| 64 |
P（ξ=3）=
| C | 3 3 |
| 3 |
| 4 |
| 27 |
| 64 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 64 |
| 9 |
| 64 |
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 4 |
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，在历年高考中都是必考题型之一．
练习册系列答案
相关题目
已知全集U={1，2，3，4，5，6}，集合M={2，3，5}，N={4，5}，则∁U（M∪N）的元素个数有（ ）
| A、0个 | B、1个 | C、2 | D、3个 |
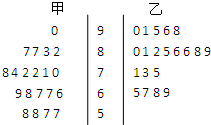为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）．如图所示茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．