题目内容
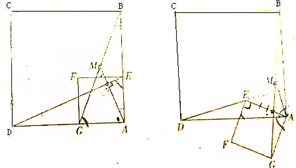 图1和图2中的四边形ABCD和AEFG都是正方形.
图1和图2中的四边形ABCD和AEFG都是正方形.(1)如图1,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
考点:函数的最值及其几何意义
专题:计算题,作图题,空间位置关系与距离
分析:(1)设AM∩DE=O,根据图形可判断Rt△DAE≌Rt△BAG,利用对应角,边长,得出∠OEA+∠EAO=90°,即可得出垂直,相等问题;
(2)延长AM到N,使MN=AM,连结NG,根据图形可判断△MNG≌△ABM,△AGN≌△DAE,再由角的转化可得∠ADE+∠DAN=90°,从而证明.
(2)延长AM到N,使MN=AM,连结NG,根据图形可判断△MNG≌△ABM,△AGN≌△DAE,再由角的转化可得∠ADE+∠DAN=90°,从而证明.
解答:
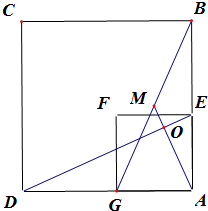 解:(1)如图1,可得出AM=
解:(1)如图1,可得出AM=
DE,AM⊥DE,证明如下,
设AM∩DE=O,
根据图形可判断Rt△DAE≌Rt△BAG,
∴∠BGA=∠DEA,∠EDA=∠GBA,DE=BG;
∵M为线段BG的中点,
∴MA=AB,AM=
BG,
∴∠MAB=∠MBA,AM=
DE,
∴∠OEA+∠EAO=90°,
∴∠EOA=90°,
∴AM⊥DE,
故AM=
DE,AM⊥DE;
(2)可得出AM=
DE,AM⊥DE,证明如下,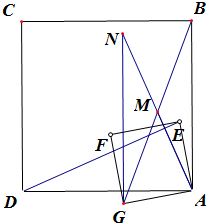
延长AM到N,使MN=AM,连结NG,
∵MN=AM,BM=MG,∠NMG=∠BMA;
∴△MNG≌△ABM;
∴NG=AB=AD,AB∥NG,
∴NG⊥AD,
∴∠AGN=∠EAD,
又∵AE=AG,
∴△AGN≌△DAE,
∴AN=DE,
∴AM=
AN=
DE;
∠ADE=∠ANG,∠DAN+∠ANG=90°,
故∠ADE+∠DAN=90°,
故AM⊥DE.
 解:(1)如图1,可得出AM=
解:(1)如图1,可得出AM=| 1 |
| 2 |
设AM∩DE=O,
根据图形可判断Rt△DAE≌Rt△BAG,
∴∠BGA=∠DEA,∠EDA=∠GBA,DE=BG;
∵M为线段BG的中点,
∴MA=AB,AM=
| 1 |
| 2 |
∴∠MAB=∠MBA,AM=
| 1 |
| 2 |
∴∠OEA+∠EAO=90°,
∴∠EOA=90°,
∴AM⊥DE,
故AM=
| 1 |
| 2 |
(2)可得出AM=
| 1 |
| 2 |

延长AM到N,使MN=AM,连结NG,
∵MN=AM,BM=MG,∠NMG=∠BMA;
∴△MNG≌△ABM;
∴NG=AB=AD,AB∥NG,
∴NG⊥AD,
∴∠AGN=∠EAD,
又∵AE=AG,
∴△AGN≌△DAE,
∴AN=DE,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
∠ADE=∠ANG,∠DAN+∠ANG=90°,
故∠ADE+∠DAN=90°,
故AM⊥DE.
点评:本题考查了平面图形中边角的关系判断与证明,同时考查了学生的作图能力,属于中档题.

练习册系列答案
相关题目
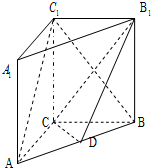 如图,在三棱柱ABC-A1B1C1中,侧棱A1A垂直于底面ABC,AC=3,BC=4,AB=5,AA1=4点D是AB的中点,
如图,在三棱柱ABC-A1B1C1中,侧棱A1A垂直于底面ABC,AC=3,BC=4,AB=5,AA1=4点D是AB的中点, 已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
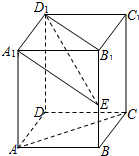 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为