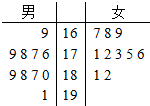
题目内容
cos
= ．
| 31π |
| 6 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用三角函数的诱导公式化为锐角的三角函数．
解答：
解：cos
=cos（4π+
）=cos
=cos（π+
）=-cos
=-
；
故答案为：-
．
| 31π |
| 6 |
| 7π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
故答案为：-
| ||
| 2 |
点评：本题考查了利用三角函数的诱导公式求三角函数值；关键是熟练诱导公式．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
对于连续不间断的函数y=f（x），定义面积函数y=∫
f（x）为直线x=a，x=b，y=0与y=f（x）围成的图形的面积，则∫
x+∫
（2x-4）-∫
log2x的值为（ ）
b a |
4 0 |
2 0 |
4 1 |
| A、6 | B、8 | C、9 | D、10 |
设函数f（x）=xlnx，则（ ）
| A、x=1为f（x）的极大值点 | ||
| B、x=1为f（x）的极小值点 | ||
C、x=
| ||
D、x=
|
已知全集U={0，1，2，3，4}，M={0，1，2}，N={2，3}，则（CUM）∩N=（ ）
| A、{2} |
| B、{3} |
| C、{2，3，4} |
| D、{0，1，2，3，4} |
连续函数y=f（x）在点x0取极值是f′（x0）=0的（ ）
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、必要非充分条件 |
