题目内容
已知动点M与点F(
,0)的距离和它到直线l:x=-
的距离相等,记点M的轨迹为曲线C1.
(1)求曲线C1的方程.
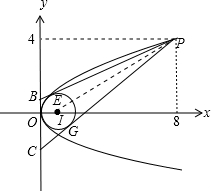
(2)设P(x0,y0)是曲线C1上的动点,点B、C在y轴上,PB,PC分别与圆(x-1)2+y2=1相切于两点E,G.
(I)当y0=4时,求|EG|;
(Ⅱ)当x0>2时,求△PBC面积的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求曲线C1的方程.
(2)设P(x0,y0)是曲线C1上的动点,点B、C在y轴上,PB,PC分别与圆(x-1)2+y2=1相切于两点E,G.
(I)当y0=4时,求|EG|;
(Ⅱ)当x0>2时,求△PBC面积的最小值.
考点:直线与圆锥曲线的综合问题,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)设出动点坐标,由已知列距离等式,代入坐标后整理得答案;
(2)(Ⅰ)求出P点的坐标,进一步求出以P和圆(x-1)2+y2=1的圆心连线为直径的圆,两圆方程作差求出过两切点的直线方程,再由点到直线的距离公式求出已知圆心到过两切点直线方程的距离,由圆的半径、弦心距和半弦长的关系求解|EG|;
(Ⅱ)设出B,C的坐标,求出直线BC的方程,由已知圆的圆心到直线的距离等于圆的半径得到(x0-2)b2+2y0b-x0=0,同理得到(x0-2)c2+2y0c-x0=0.说明b,c是方程
(x0-2)x2+2y0x-x0=0的两根.由求根公式求出b,c的值,作差后得到b-c,代入三角形的面积公式后利用基本不等式求△PBC面积的最小值.
(2)(Ⅰ)求出P点的坐标,进一步求出以P和圆(x-1)2+y2=1的圆心连线为直径的圆,两圆方程作差求出过两切点的直线方程,再由点到直线的距离公式求出已知圆心到过两切点直线方程的距离,由圆的半径、弦心距和半弦长的关系求解|EG|;
(Ⅱ)设出B,C的坐标,求出直线BC的方程,由已知圆的圆心到直线的距离等于圆的半径得到(x0-2)b2+2y0b-x0=0,同理得到(x0-2)c2+2y0c-x0=0.说明b,c是方程
(x0-2)x2+2y0x-x0=0的两根.由求根公式求出b,c的值,作差后得到b-c,代入三角形的面积公式后利用基本不等式求△PBC面积的最小值.
解答:
 解:(1)设动点M的坐标为(x,y),由题意可知,|MF|=|x+
解:(1)设动点M的坐标为(x,y),由题意可知,|MF|=|x+
|,
即
=|x+
|,
化简得:y2=2x.
∴曲线C1的方程为y2=2x.
(2)(Ⅰ)当y0=4时,点P坐标为(8,4),
如图,设圆(x-1)2+y2=1的圆心为I(1,0),
过P作圆I的两条切线分别切圆与E,G两点,
∴E,G两点都在以线段PI为直径的圆上.
由
•
=0,得以PI为直径的圆的方程是(x-1)(x-8)+y(y-4)=0.
而EG是圆(x-1)2+y2=1及圆(x-1)(x-8)+y(y-4)=0的公共弦.
两圆相减得EG的方程:7x+4y-8=0.
圆心I(1,0)到直线7x+4y-8=0的距离是d=
=
.
∴|EG|=2
=2
=
=
;
(Ⅱ)设P(x0,y0),B(0,b),C(0,c),不妨设b>c,
直线PB的方程:y-b=
x,化简得:(y0-b)x-x0y+x0b=0.
又圆心(1,0)到PB的距离为1,则
=1,
故(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
∵x0>2,上式化简得(x0-2)b2+2y0b-x0=0.
同理有(x0-2)c2+2y0c-x0=0.
∴b,c是方程(x0-2)x2+2y0x-x0=0的两根.
由求根公式得:x=
=
.
从而(b-c)2=
.
∵P(x0,y0)是抛物线上的点,有y02=2x0,
则(b-c)2=
,b-c=
.
∴S△PBC=
(b-c)x0=
•x0=(x0-2)+
+4≥8.
当(x0-2)2=4时,上式取等号,此时x0=4,y0=±2
.
因此S△PBC的最小值为8.
 解:(1)设动点M的坐标为(x,y),由题意可知,|MF|=|x+
解:(1)设动点M的坐标为(x,y),由题意可知,|MF|=|x+| 1 |
| 2 |
即
(x-
|
| 1 |
| 2 |
化简得:y2=2x.
∴曲线C1的方程为y2=2x.
(2)(Ⅰ)当y0=4时,点P坐标为(8,4),
如图,设圆(x-1)2+y2=1的圆心为I(1,0),
过P作圆I的两条切线分别切圆与E,G两点,
∴E,G两点都在以线段PI为直径的圆上.
由
| PG |
| GI |
而EG是圆(x-1)2+y2=1及圆(x-1)(x-8)+y(y-4)=0的公共弦.
两圆相减得EG的方程:7x+4y-8=0.
圆心I(1,0)到直线7x+4y-8=0的距离是d=
| |7-8| | ||
|
| 1 | ||
|
∴|EG|=2
| r2-d2 |
1-
|
| 16 | ||
|
| 16 |
| 65 |
| 65 |
(Ⅱ)设P(x0,y0),B(0,b),C(0,c),不妨设b>c,
直线PB的方程:y-b=
| y0-b |
| x0 |
又圆心(1,0)到PB的距离为1,则
| |y0-b+x0b| | ||
|
故(y0-b)2+x02=(y0-b)2+2x0b(y0-b)+x02b2,
∵x0>2,上式化简得(x0-2)b2+2y0b-x0=0.
同理有(x0-2)c2+2y0c-x0=0.
∴b,c是方程(x0-2)x2+2y0x-x0=0的两根.
由求根公式得:x=
-2y0±
| ||
| 2(x0-2) |
-y0±
| ||
| x0-2 |
从而(b-c)2=
| 4x02+4y02-8x0 |
| (x0-2)2 |
∵P(x0,y0)是抛物线上的点,有y02=2x0,
则(b-c)2=
| 4x02 |
| (x0-2)2 |
| 2x0 |
| x0-2 |
∴S△PBC=
| 1 |
| 2 |
| x0 |
| x0-2 |
| 4 |
| x0-2 |
当(x0-2)2=4时,上式取等号,此时x0=4,y0=±2
| 2 |
因此S△PBC的最小值为8.
点评:本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,这也是高考常考的知识点.考查了学生的计算能力,是压轴题.

练习册系列答案
相关题目
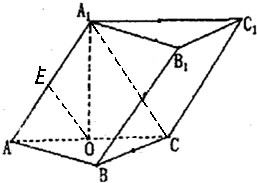 如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.
如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.