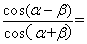题目内容
已知点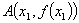 ,
,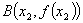 是函数
是函数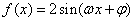
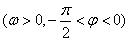 图象上的任意两点,且角
图象上的任意两点,且角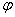 的终边经过点
的终边经过点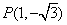 ,若
,若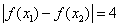 时,
时,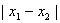 的最小值为
的最小值为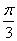 .
.
(1)求函数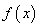 的解析式;
的解析式;
(2)求函数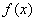 的单调递增区间;
的单调递增区间;
(3)当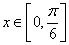 时,不等式
时,不等式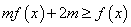 恒成立,求实数
恒成立,求实数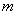 的取值范围.
的取值范围.
解:(1)角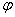 的终边经过点
的终边经过点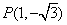 ,
, ,
,
 ,
, .
.
由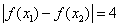 时,
时,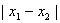 的最小值为
的最小值为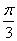 ,
,
得 ,即
,即 ,
,
∴
(2) ,即
,即 ,
,
 函数
函数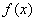 的单调递增区间为
的单调递增区间为

(3 ) 当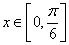 时,
时, ,
,
于是, ,
,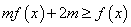
等价于
由  , 得
, 得 的最大值为
的最大值为
所以,实数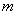 的取值范围是
的取值范围是 。
。
注:用别的方法求得 ,只要正确就给3分。
,只要正确就给3分。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围. ,当
,当 时,不等式
时,不等式
 恒成立,则整数
恒成立,则整数 的最大值为
的最大值为  ,
, ,则
,则 _ ____
_ ____
 ,函数
,函数 在区间
在区间 上的最大值等于
上的最大值等于 ,则
,则 的值为 .
的值为 .  ,则
,则 = .
= . 中,P,M分别为线段
中,P,M分别为线段 ,
, 上的点,若
上的点,若 ,则三棱锥
,则三棱锥 的体积为 .
的体积为 . ,
, ,则
,则 .
.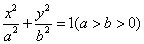 的离心率
的离心率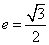 ,A,B是椭圆的左、右顶点,P是椭圆上不同于A,B的一点,直线PA,PB倾斜角分别为
,A,B是椭圆的左、右顶点,P是椭圆上不同于A,B的一点,直线PA,PB倾斜角分别为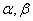 ,则
,则