题目内容
16.已知△ABC的三个内角A,B,C的对边分别为a,b,c,若b=c-2bcosA.(1)求证:A=2B;
(2)若5b=3c,$a=4\sqrt{6}$,求BC边上的高.
分析 (1)因为b=c-2bcosA,所以sinB=sinC-2sinBcosA,进而sinB=sin(A-B),即可证明结论;
(2)由余弦定理,求出b=6,c=10,利用等面积求BC边上的高.
解答 (1)证明:因为b=c-2bcosA,
所以sinB=sinC-2sinBcosA,
因为C=π-(B+A),
所以sinB=sin(π-(B+A))-2sinBsinA
所以sinB=sinBcosA+cosBsinA-2sinBcosA
即sinB=cosBsinA-sinBcosA,
即sinB=sin(A-B),
因为0<B<π,0<A<π,所以-π<A-B<π,
所以B=A-B或B=π-(A-B),
故A=2B;
(2)解:由5b=3c及b=c-2bcosA得,$cosA=\frac{1}{3}$,
由余弦定理:a2=b2+c2-2bccosA得${(4\sqrt{6})^2}={b^2}+{(\frac{5}{3}b)^2}-2b×\frac{5}{3}b×\frac{1}{3}$,
解得:b=6,c=10,
由$cosA=\frac{1}{3}$得,$sinA=\frac{2}{3}\sqrt{2}$,
设BC边上的高为h,则$\frac{1}{2}×bcsinA=\frac{1}{2}×ah$,
即$6×10×\frac{2}{3}\sqrt{2}=4\sqrt{6}h$,
所以$h=\frac{10}{3}\sqrt{3}$.
点评 本题考查三角形中的几何计算,考查余弦定理的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
7.设集合A={x|x≤0或x≥2},B={x|x<1},则集合A∩B=( )
| A. | (-∞,0) | B. | (-∞,0] | C. | [2,+∞) | D. | (2,+∞) |
4.如图,正方形ABCD中,AC与BD交于O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,若$\overrightarrow{BD}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{OF}$,则λ+μ的值为( )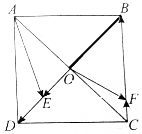

| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
1.定义“函数y=f(x)是D上的a级类周期函数”如下:函数y=f(x),x∈D,对于给定的非零常数 a,总存在非零常数T,使得定义域D内的任意实数x都有af(x)=f(x+T)恒成立,此时T为f(x)的周期.若y=f(x)是[1,+∞)上的a级类周期函数,且T=1,当x∈[1,2)时,f(x)=2x+1,且y=f(x)是[1,+∞)上的单调递增函数,则实数a的取值范围为( )
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{5}{3},+∞})$ | D. | [10,+∞) |
6.若等比数列{an},前n项和Sn,且a2a3=2a1,$\frac{5}{4}$为a4与2a7的等差中项,则S4=( )
| A. | 29 | B. | 30 | C. | 31 | D. | 33 |
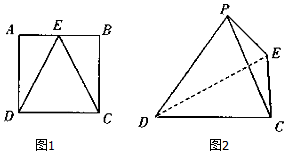 如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.