��Ŀ����
1�����塰����y=f��x����D�ϵ�a�������ں��������£�����y=f��x����x��D�����ڸ����ķ��㳣�� a���ܴ��ڷ��㳣��T��ʹ�ö�����D�ڵ�����ʵ��x����af��x��=f��x+T�����������ʱTΪf��x�������ڣ���y=f��x����[1��+�ޣ��ϵ�a�������ں�������T=1����x��[1��2��ʱ��f��x��=2x+1����y=f��x����[1��+�ޣ��ϵĵ���������������ʵ��a��ȡֵ��ΧΪ��������| A�� | $[{\frac{5}{6}��+��}��$ | B�� | [2��+�ޣ� | C�� | $[{\frac{5}{3}��+��}��$ | D�� | [10��+�ޣ� |
���� ���ú���a�������ڵĶ������μ���f��x���ڸ��������ϵĽ���ʽ������f��x����[n��n+1���ϵĽ���ʽ�����ú����ĵ������г�����ʽ���ɵó�a�ķ�Χ��
��� �⣺��x��[1��2��ʱ��f��x��=2x+1��
�൱x��[2��3��ʱ��f��x��=af��x-1��=a•[2��x-1��+1]��
��
��x��[n��n+1��ʱ��f��x��=af��x-1��=a2f��x-2��=��=an-1f��x-n+1��=an-1•[2��x-n+1��+1]��
��x��[n��n+1��ʱ��f��x��=an-1•[2��x-n+1��+1]��n��N*��
�൱x��[n-1��n��ʱ��f��x��=an-2•[2��x-n+1+1��+1]=an-2•[2��x-n+2��+1]��
��f��x����[1��+�ޣ��ϵ���������
��an-2•5��an-1•3�������
��a��$\frac{5}{3}$��
��ѡC��
���� ���⿼���˺�������ʽ����⣬�ֶκ��������Ե�Ӧ�ã������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
11���������������̹������ƣ�����Բ������һ���������硢�ٰ�磬����ǧ�������ܼ��Σ���һԲ���ιȲ֣���1��3��$3\frac{1}{3}$�磬������2000����1��=10�ߣ�1��=10�磬��Ϊ�ݻ���λ��1����1.62�����ߣ��С�3������Բ������Բ���ܳ�ԼΪ��������
| A�� | 1��3�� | B�� | 5��4�� | C�� | 9��2�� | D�� | 48 |
12���ڵ���������ABC�У���A=150�㣬AC=AB=1����$\overrightarrow{AB}•\overrightarrow{BC}$=��������
| A�� | $-\frac{{\sqrt{3}}}{2}-1$ | B�� | $-\frac{{\sqrt{3}}}{2}+1$ | C�� | $\frac{{\sqrt{3}}}{2}-1$ | D�� | $\frac{{\sqrt{3}}}{2}+1$ |
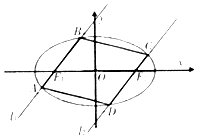 ��ͼ������ԲC��$\frac{{x}^{2}}{4}$+y2=1�����ҽ���F1��F2�ֱ���ֱ��l1��l2����Բ��A��B��C��D����l1��l2��
��ͼ������ԲC��$\frac{{x}^{2}}{4}$+y2=1�����ҽ���F1��F2�ֱ���ֱ��l1��l2����Բ��A��B��C��D����l1��l2�� ��ͼ��������P-ABCD�У�����ABCD�������Σ�PA�͵���ABCD��PA=PB��E��F�ֱ���PA��PB���е㣮
��ͼ��������P-ABCD�У�����ABCD�������Σ�PA�͵���ABCD��PA=PB��E��F�ֱ���PA��PB���е㣮