题目内容
4.如图,正方形ABCD中,AC与BD交于O,$\overrightarrow{BE}$=$\frac{3}{4}$$\overrightarrow{BD}$,$\overrightarrow{CF}$=$\frac{1}{4}$$\overrightarrow{CB}$,若$\overrightarrow{BD}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{OF}$,则λ+μ的值为( )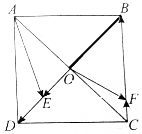
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
分析 以D为坐标原点,建立如图所示的直角坐标系,设正方形的边长为4,分别表示出各点的坐标,再根据$\overrightarrow{BD}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{OF}$,得到关于λ,μ的方程组解得即可.
解答  解:以D为坐标原点,建立如图所示的直角坐标系,设正方形的边长为4,
解:以D为坐标原点,建立如图所示的直角坐标系,设正方形的边长为4,
∴B(4,4),A(0,4),E(1,1),O(2,2),F(4,1),
∴$\overrightarrow{BD}$=(-4,-4),$\overrightarrow{AE}$=(1,-3),$\overrightarrow{OF}$=(2,-1),
∵$\overrightarrow{BD}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{OF}$,
∴(-4,-4)=(λ,-3λ)+(2μ,-μ)=(λ+2μ,-3λ-μ),
∴$\left\{\begin{array}{l}{λ+2μ=-4}\\{-3λ-μ=-4}\end{array}\right.$,
解得λ=$\frac{12}{5}$,μ=-$\frac{16}{5}$,
∴λ+μ=-$\frac{4}{5}$,
故选:D
点评 本题考查了向量坐标的是运算,关键是构造平面直角坐标系,属于中档题

练习册系列答案
相关题目
15.如图中网格纸的小正方形的边长是1,复平面内点Z所表示的复数z满足(z1-i)•z=1,则复数z1=( )
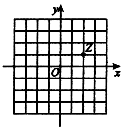

| A. | -$\frac{2}{5}+\frac{4}{5}$i | B. | $\frac{2}{5}+\frac{4}{5}$i | C. | $\frac{2}{5}-\frac{4}{5}$i | D. | -$\frac{2}{5}-\frac{4}{5}$i |
12.在等腰三角形ABC中,∠A=150°,AC=AB=1,则$\overrightarrow{AB}•\overrightarrow{BC}$=( )
| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |
14.设[x]表示不小于实数x的最小整数,如[2.6]=3,[-3.5]=-3.已知函数f(x)=[x]2-2[x],若函数F(x)=f(x)-k(x-2)+2在(-1,4]上有2个零点,则k的取值范围是( )
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $[{-1,-\frac{2}{3}})∪[5,10)$ | C. | $({-\frac{4}{3},-1}]∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.