题目内容
7.设集合A={x|x≤0或x≥2},B={x|x<1},则集合A∩B=( )| A. | (-∞,0) | B. | (-∞,0] | C. | [2,+∞) | D. | (2,+∞) |
分析 根据交集的定义写出集合A∩B.
解答 解:集合A={x|x≤0或x≥2},B={x|x<1},
则集合A∩B={x|x≤0}=(-∞,0].
故选:B.
点评 本题考查了交集的运算问题,是基础题.

练习册系列答案
相关题目
15.如图中网格纸的小正方形的边长是1,复平面内点Z所表示的复数z满足(z1-i)•z=1,则复数z1=( )
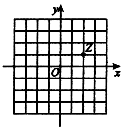

| A. | -$\frac{2}{5}+\frac{4}{5}$i | B. | $\frac{2}{5}+\frac{4}{5}$i | C. | $\frac{2}{5}-\frac{4}{5}$i | D. | -$\frac{2}{5}-\frac{4}{5}$i |
2.已知直线x+y-a=0与圆x2+y2=2交于A、B两点,O点坐标原点,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$满足条件$|{2\overrightarrow{OA}-3\overrightarrow{OB}}|=|{2\overrightarrow{OA}+3\overrightarrow{OB}}|$,则实数a的值为( )
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | ±1 | D. | $±\sqrt{2}$ |
12.在等腰三角形ABC中,∠A=150°,AC=AB=1,则$\overrightarrow{AB}•\overrightarrow{BC}$=( )
| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |