题目内容
7.已知直线l1:3x+2y-1=0,直线l2:5x+2y+1=0,直线l3:3x-5y+6=0,直线L经过直线l1与直线l2的交点,且垂直于直线l3,求直线L的一般式方程.分析 解得l1、l2的交点 (-1,2),再根据两直线垂直,斜率之积等于-1求得直线l的斜率,用点斜式求得直线l的方程.
解答 解:由$\left\{\begin{array}{l}{3x+2y-1=0}\\{5x+2y+1=0}\end{array}\right.$,解得l1、l2的交点 (-1,2),
∵垂直于直线l3,
∴直线L的斜率k=-$\frac{5}{3}$,
∴直线方程为y-2=-$\frac{5}{3}$(x+1)
即直线l的一般式方程为:5x+3y-1=0.
点评 本题考查了相互垂直的直线斜率之间的关系、直线的交点,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.两条直线l1:ax+(1+a)y=3,l2:(a+1)x+(3-2a)y=2互相垂直,则a的值是 ( )
| A. | 3 | B. | -1 | C. | -1或3 | D. | 0 或 3 |
2.已知函数f(x)=|x2+bx|(b∈R),当x∈[0,1]时,f(x)的最大值为M(b),则M(b)的最小值是( )
| A. | 3-2$\sqrt{2}$ | B. | 4-2$\sqrt{3}$ | C. | 1 | D. | 5-2$\sqrt{5}$ |
19.若数列{an}满足a1=$\sqrt{3}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$([an]与{an}分别表示an的整数部分与小数部分),则a2016=( )
| A. | 3023+$\sqrt{3}$ | B. | 3023+$\frac{\sqrt{3}-1}{2}$ | C. | 3020+$\sqrt{3}$ | D. | 3020+$\frac{\sqrt{3}-1}{2}$ |
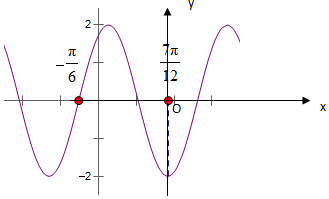 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.