题目内容
10.已知实数x,y满足约束条件$\left\{\begin{array}{l}{y-x+1≥0}\\{2y-kx-8≤0}\\{ky+2x-2≤0}\end{array}\right.$,若目标函数z=y-x既存在最大值,又存在最小值,则实数k的取值范围为( )| A. | (-∞,1] | B. | (-∞,2] | C. | [1,2] | D. | [2,+∞) |
分析 令k=0,k=4等特殊值,做出平面区域,观察目标函数是否存在最大值和最小值即可判断出选项.
解答 解:由z=y-x得y=x+z,
当k=0时,作出平面区域如图:
由图形可知y=x+z在y轴上的截距没有最大值,故k≠0,排除A,B;
当k=4时,作出平面区域如图:
由图形可知y=x+z在y轴上的截距既有最大值也有最小值,符合题意,排除C.
故选D.
点评 本题考查了简单的线性规划,作出平面区域,观察目标函数是否有最优解是关键.

练习册系列答案
相关题目
1.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是( )
| A. | 至少有1个黑球与都是红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
19.设f(1-x)=$\frac{x+1}{2x-1}$,则f(x)=( )
| A. | $\frac{x}{2x-1}$ | B. | $\frac{x-2}{1-2x}$ | C. | $\frac{x+1}{2x-1}$ | D. | $\frac{2-x}{1-2x}$ |
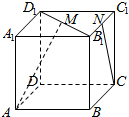 正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.