题目内容
20.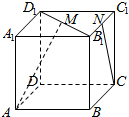 正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AM和CN所成角的余弦值.
解答 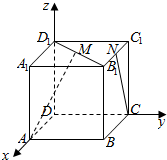 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A(2,0,0),M(1,1,2),C(0,2,0),N(1,2,2),
$\overrightarrow{AM}$=(-1,1,2),$\overrightarrow{CN}$=(1,0,2),
设异面直线AM和CN所成角为θ,
则cosθ=$\frac{|\overrightarrow{AM}•\overrightarrow{CM}|}{|\overrightarrow{AM}|•|\overrightarrow{CM}|}$=$\frac{3}{\sqrt{6}•\sqrt{5}}$=$\frac{\sqrt{30}}{10}$.
∴异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
故答案为:$\frac{\sqrt{30}}{10}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
10.若向量$\overrightarrow{a}$=(x,4,5),$\overrightarrow{b}$=(1,-2,2)且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{\sqrt{2}}{6}$,则x的值为 ( )
| A. | 3 | B. | 3或-11 | C. | -3 | D. | -3或11 |
5.某产品的广告费x(万元)与销售额y(万元)的统计数据如表:
由最小二乘法可得回归方程$\widehat{y}$=7x+a,据此预测,当广告费用为7万元时,销售额约为( )
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 20 | 30 | 40 | 50 |
| A. | 56万元 | B. | 58万元 | C. | 68万元 | D. | 70万元 |