题目内容
1.函数y=4sinx-cos2x(x∈[-$\frac{π}{6}$,$\frac{π}{6}$])的值域是[$-\frac{5}{2}$,$\frac{3}{2}$].分析 利用二倍角的余弦公式变形化简函数解析式,由换元法、正弦函数、二次函数的性质求出值域.
解答 解:由题意得,y=4sinx-cos2x=4sinx-(1-2sin2x)
=2sin2x+4sinx-1,
设t=sinx,由x∈[-$\frac{π}{6}$,$\frac{π}{6}$]得t∈[$-\frac{1}{2}$,$\frac{1}{2}$],
则原函数变为:y=2t2+4t-1=2(t+1)2-3,
又函数y=2t2+4t-1在[$-\frac{1}{2}$,$\frac{1}{2}$]上递增,
则当t=$-\frac{1}{2}$时,函数取到最小值是:$2{(-\frac{1}{2}+1)}^{2}-3$=$-\frac{5}{2}$,
当t=$\frac{1}{2}$时,函数取到最大值是:$2{(\frac{1}{2}+1)}^{2}-3$=$\frac{3}{2}$,
所以函数的值域是[$-\frac{5}{2}$,$\frac{3}{2}$],
故答案为:[$-\frac{5}{2}$,$\frac{3}{2}$].
点评 本题考查了正弦函数、二次函数的性质,二倍角的余弦公式,以及换元法求函数的值域,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
11.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=( )
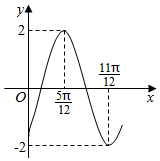

| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
12.如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
| A. | -2<a<2 | B. | $\sqrt{3}<a≤2$ | C. | $-\sqrt{3}<a≤2$ | D. | $-\sqrt{3}≤a≤2$ |
9.“mn<0”是“方程mx2+ny2=1表示焦点在y轴上的双曲线”的( )
| A. | 充分必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分而不必要条件 | D. | 必要而不充分条件 |
6.已知一个样本中的数据为1,2,3,4,5,则该样本的方差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |