题目内容

16．已知函数f（x）=$\left\{\begin{array}{l}{{a}^{x}+1，x≤0}\\{|lnx|，x＞0}\end{array}\right.$当1＜a＜2时，关于x的方程f[f（x）]=a实数解的个数为（　　）
A．2B．3C．4D．5

分析 判断f（x）的单调性，做出f（x）的草图，得出f（t）=a的根的情况，再根据方程f（x）=t的根个数，得出结论．

解答 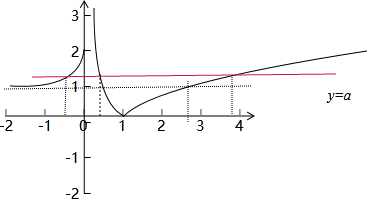解：函数f（x）=$\left\{\begin{array}{l}{{a}^{x}+1，x≤0}\\{|lnx|，x＞0}\end{array}\right.$的图象如下，令f（t）=a，
∵1＜a＜2，如图所示得，方程f（t）=a有三个根：t1，t2，t3．
且t1＜0，${t}_{2}∈（{e}^{-2}，{e}^{-1}）$，${t}_{3}∈（e，{e}^{2}）$．
方程f（x）=t1无解，方程f（x）=t2有两个解，方程f（x）=t3无解．
故关于x的方程f[f（x）]=a实数解的个数为2，
故选：A．

点评 本题考查了复合函数根的存在性判断，数形结合思想，属于中档题

练习册系列答案
相关题目
6．设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1（a＞0）的渐近线方程为3x+2y=0，则a的值为（　　）
A．4B．3C．2D．1
7．已知函数f（x）=|x-a|-|x-4|（x∈R，a∈R）的值域为[-3，3]．
（Ⅰ）求实数a的值；
（Ⅱ）若存在x0∈R，使得f（x0）≤2m-m2，求实数m的取值范围．
4．已知△ABC中，内角A，B，C的对边分别为a，b，c，b=2，B=45°，若三角形有两解，则a的取值范围是（　　）
A．a＞2B．0＜a＜2C．2＜a＜2$\sqrt{2}$D．2＜a＜2$\sqrt{3}$
11．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，点P（1，$\frac{\sqrt{2}}{2}$）在椭圆E上，直线l过椭圆的右焦点F且与椭圆相交于A，B两点．
（1）求E的方程；
（2）在x轴上是否存在定点M，使得$\overrightarrow{MA}$•$\overrightarrow{MB}$为定值？若存在，求出定点M的坐标；若不存在，说明理由．
1．若x，y满足$\left\{\begin{array}{l}{y-1≥0}\\{x-y+1≥0}\\{x-1≤0}\end{array}\right.$，则x+y的最小值是（　　）
A．-1B．1C．2D．3
8．双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的右焦点为（2，0）．则此双曲线的渐近线方程为y=±$\sqrt{3}$x．
5．已知函数f（x）=-x3+ax2-x-2在（-∞，+∞）上是单调函数，则实数a的取值范围是（　　）
A．（-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞）B．（-$\sqrt{3}$，$\sqrt{3}$）C．（-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞）D．[-$\sqrt{3}$，$\sqrt{3}$]
6．设直线x-y-a=0与圆x2+y2=4相交于A，B两点，O为坐标原点，若△AOB为等边三角形，则实数a的值为（　　）
A．$±\sqrt{3}$B．$±\sqrt{6}$C．±3D．±9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网