题目内容
已知命题“直线 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题:
①直线 上的点都在平面
上的点都在平面 内;
内;
②直线 上有些点不在平面
上有些点不在平面 内;
内;
③平面 内任意一条直线都不与直线
内任意一条直线都不与直线 平行.
平行.
其中真命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
D
解析试题分析:因为,命题“直线 与平面
与平面 有公共点”是真命题,即包括了两种情况,
有公共点”是真命题,即包括了两种情况,
一是直线 与平面
与平面 有一个公共点---相交;
有一个公共点---相交;
二是,直线 与平面
与平面 有无数多公共点---直线在平面内.
有无数多公共点---直线在平面内.
所以,①直线 上的点都在平面
上的点都在平面 内,是假命题;②直线
内,是假命题;②直线 上有些点不在平面
上有些点不在平面 内,是假命题;
内,是假命题;
③平面 内任意一条直线都不与直线
内任意一条直线都不与直线 平行,是假命题.
平行,是假命题.
故选D.
考点:直线与平面

练习册系列答案
相关题目
设 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C. , , ,则 ,则 | D.若 , , ,则 ,则 |
棱长为1的正方体ABCD A1B1C1D1中,点M,N分别在线段AB1,BC1上,且AM=BN,给出以下结论:
①AA1⊥MN
②异面直线AB1,BC1所成的角为60°
③四面体B1 D1CA的体积为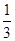
④A1C⊥AB1,A1C⊥BC1, 其中正确的结论的个数为( ) 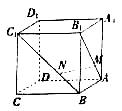
| A.1 | B.2 | C.3 | D.4 |
设 是两条不同直线,
是两条不同直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( )
A. 且 且 则 则 | B. 且 且 ,则 ,则 |
C. 则 则 | D. 则 则 |
已知两个不同的平面 和两条不重合的直线
和两条不重合的直线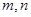 ,则下列命题不正确的是 ( )
,则下列命题不正确的是 ( )
A.若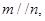 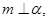 则 则 |
B.若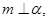 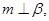 则 则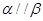 |
C.若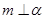 , ,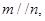 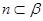 ,则 ,则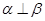 |
D.若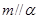 , ,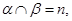 ,则 ,则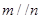 |
三棱柱 中,
中, 与
与 、
、 所成角均为
所成角均为 ,
, ,且
,且 ,则三棱锥
,则三棱锥 的体积为( )
的体积为( )
A. | B. | C. | D. |
已知三棱锥S-ABC,G1,G2分别为△SAB,△SAC的重心,则G1G2与△SBC,△ABC所在平面的位置关系是 ( )
| A.垂直和平行 | B.均为平行 | C.均为垂直 | D.不确定 |
设 、
、 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题中,正确的是( )
是一条直线,以下命题中,正确的是( )
A.若 , , ,则 ,则 | B.若 , ,  ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
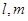 ,平面
,平面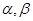 ,且
,且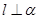 ,
,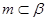 ,给出下列四个命题:
,给出下列四个命题: ∥
∥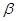 ,则
,则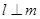 ;
;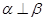 ,则
,则 ∥
∥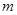 ;
;