题目内容
已知三棱锥S-ABC,G1,G2分别为△SAB,△SAC的重心,则G1G2与△SBC,△ABC所在平面的位置关系是 ( )
| A.垂直和平行 | B.均为平行 | C.均为垂直 | D.不确定 |
B
解析试题分析:根据题意,由于三棱锥S-ABC,G1,G2分别为△SAB,△SAC的重心,则G1G2与△SBC,△ABC所在平面的位置关系是,利用中位线性质定理,可知线线平行,得到线面平行,选B.
考点:线面平行
点评:主要是考查了线面平行的判定,属于基础题。

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
在下列条件下,可判断平面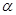 与平面
与平面 平行的是( )
平行的是( )
| A.α、β都垂直于平面γ |
| B.α内不共线的三个点到β的距离相等 |
| C.l,m是α内两条直线且l∥β,m∥β |
| D.l,m是异面直线,且l∥α,m∥α,l∥β,m∥β |
设 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,则下列命题不正确的是( )
是三个不同的平面,则下列命题不正确的是( )
A.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , ,   ,则 ,则 ∥ ∥ |
D.若 ∥ ∥ , , ∥ ∥ ,则 ,则 不一定平行于 不一定平行于 |
如图,二面角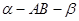 与
与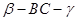 均为
均为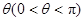 ,
,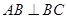 ,
,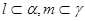 ,则下列不可能成立的是( )
,则下列不可能成立的是( )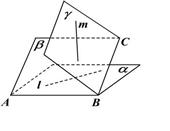
A.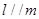 | B.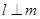 |
C.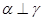 | D.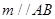 |
在棱长为 的正方体
的正方体 中,错误的是( )
中,错误的是( )
A.直线 和直线 和直线 所成角的大小为 所成角的大小为 |
B.直线 平面 平面 |
C.二面角 的大小是 的大小是 |
D.直线 到平面 到平面 的距离为 的距离为 |
已知正四棱锥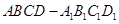 中,
中,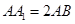 ,则CD与平面
,则CD与平面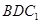 所成角的正弦值等于( )
所成角的正弦值等于( )
A.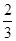 | B.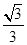 | C.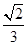 | D.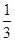 |
 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: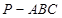 中,
中,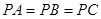 ,底面
,底面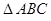 是正三角形,
是正三角形,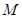 、
、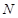 分别是侧棱
分别是侧棱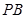 、
、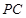 的中点.若平面
的中点.若平面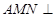 平面
平面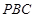 ,则平面
,则平面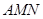 与平面
与平面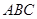 所成二面角(锐角)的余弦值等于( )
所成二面角(锐角)的余弦值等于( )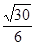
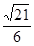
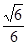
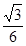

 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为 的正方形,底面中心为
的正方形,底面中心为 ,以
,以 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )


