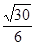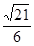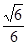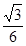题目内容
棱长为1的正方体ABCD A1B1C1D1中,点M,N分别在线段AB1,BC1上,且AM=BN,给出以下结论:
①AA1⊥MN
②异面直线AB1,BC1所成的角为60°
③四面体B1 D1CA的体积为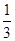
④A1C⊥AB1,A1C⊥BC1, 其中正确的结论的个数为( ) 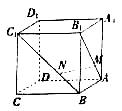
| A.1 | B.2 | C.3 | D.4 |
D
解析试题分析:连结C1D、DB、D1B1、AD,易证平面C1DB//平面D1B1A,且垂直平分A1C,则在平行四边形AB1C1D中,作ME//AD交C1D于E,连结NE,可得平面DNE//平面ABCD,可得AA1⊥MN,①对,AB1//C1D,三角形C1DB为等边三角形,则异面直线AB1,BC1所成的角为60°②正确, ,③对,A1C⊥AB1,A1C⊥BC1④正确,故选D.
,③对,A1C⊥AB1,A1C⊥BC1④正确,故选D.
考点:1.异面直线夹角;2.几何体体积

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
正方体ABCD—A1B1C1D1中直线 与平面
与平面 夹角的余弦值是( )
夹角的余弦值是( )
A. | B. | C. | D. |
在下列条件下,可判断平面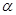 与平面
与平面 平行的是( )
平行的是( )
| A.α、β都垂直于平面γ |
| B.α内不共线的三个点到β的距离相等 |
| C.l,m是α内两条直线且l∥β,m∥β |
| D.l,m是异面直线,且l∥α,m∥α,l∥β,m∥β |
设 是两条直线,
是两条直线, 是两个平面,下列能推出
是两个平面,下列能推出 的是( )
的是( )
A. | B. |
C. | D. |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等, 则这两条直线平行; |
| B.若一个平面内有三点到另一个平面的距离相等,则这两个平面平行; |
| C.若一条直线和两个相交平面都平行, 则这条直线与这两个平面的交线平行; |
| D.若两个平面都垂直于第三个平面, 则这两个平面平行. |
设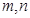 是两条不同的直线,
是两条不同的直线,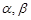 是两个不同的平面,有下列四个命题:
是两个不同的平面,有下列四个命题:
① 若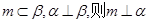 ; ② 若
; ② 若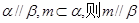 ;
;
③ 若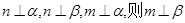 ; ④ 若
; ④ 若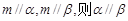
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |
已知正四棱锥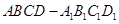 中,
中,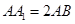 ,则CD与平面
,则CD与平面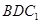 所成角的正弦值等于( )
所成角的正弦值等于( )
A.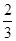 | B.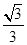 | C.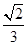 | D.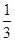 |
 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: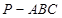 中,
中,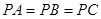 ,底面
,底面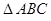 是正三角形,
是正三角形,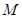 、
、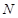 分别是侧棱
分别是侧棱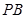 、
、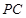 的中点.若平面
的中点.若平面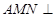 平面
平面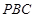 ,则平面
,则平面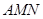 与平面
与平面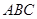 所成二面角(锐角)的余弦值等于( )
所成二面角(锐角)的余弦值等于( )