题目内容
设 、
、 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题中,正确的是( )
是一条直线,以下命题中,正确的是( )
A.若 , , ,则 ,则 | B.若 , ,  ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
C
解析试题分析:解:若l⊥α,α⊥β,则l?β或l∥β,故A错误;若l∥α,α∥β,则l?β或l∥β,故B错误;若l⊥α,α∥β,由平面平行的性质,我们可得l⊥β,故C正确;若l∥α,α⊥β,则l⊥β或l∥β,故D错误;故选C
考点:空间中线面的位置关系
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来

练习册系列答案
相关题目
在棱长为 的正方体
的正方体 中,错误的是( )
中,错误的是( )
A.直线 和直线 和直线 所成角的大小为 所成角的大小为 |
B.直线 平面 平面 |
C.二面角 的大小是 的大小是 |
D.直线 到平面 到平面 的距离为 的距离为 |
设m,n是不同的直线, 是不同的平面,下列命题中正确的是
是不同的平面,下列命题中正确的是
A.若m// |
B.若m// |
C.若m//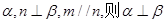 |
D.若m// |
用M表示平面, 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与 ( )
( )
| A.平行; | B.相交; | C.异面; | D.垂直。 |
若直线上有两个点在平面外,则( )
| A.直线上至少有一个点在平面内 |
| B.直线上有无穷多个点在平面内 |
| C.直线上所有点都在平面外 |
| D.直线上至多有一个点在平面内 |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若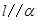 , , ,则 ,则 | D.若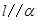 , , ,则 ,则 |
已知正四棱锥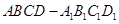 中,
中,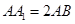 ,则CD与平面
,则CD与平面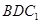 所成角的正弦值等于( )
所成角的正弦值等于( )
A.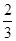 | B.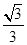 | C.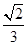 | D.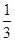 |
 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为 的正方形,底面中心为
的正方形,底面中心为 ,以
,以 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )


