题目内容
17.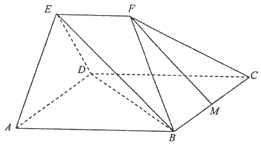 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.(1)求证:直线MF∥平面BED;
(2)求证:平面BED⊥平面EAD;
(3)求直线BF与平面BED所成角的正弦值.
分析 (1)取BD的中点G,连结MG,EG,通过证明四边形EFMG是平行四边形得出MF∥EG,从而有MF∥平面BED;
(2)取AD中点O,则OE⊥AD,根据面面垂直和线面垂直的性质得出OE⊥BD,利用勾股定理逆定理证明BD⊥AD,于是BD⊥平面ADE,从而平面BED⊥平面EAD;
(3)以O为原点建立空间坐标系,求出平面BED的法向量,通过计算法向量与$\overrightarrow{BF}$的夹角得出直线BF与平面BED所成角.
解答 证明:(1)取BD的中点G,连结MG,EG,
∵M为线段BC的中点,G是BD的中点,
∵MG$\stackrel{∥}{=}$$\frac{1}{2}$CD,又CD$\stackrel{∥}{=}AB$,EF$\stackrel{∥}{=}$$\frac{1}{2}$AB,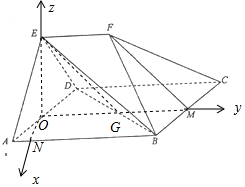
∴EF$\stackrel{∥}{=}$GM,
∴四边形EFMG是平行四边形,
∴MF∥EG,
又MF?平面BED,EG?平面BED,
∴MF∥平面BED.
(2)取AD中点O,连结EO,则OE⊥AD,
∵平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,OE?平面ADE,OE⊥AD,
∴OE⊥平面ABCD,又BD?平面ABCD,
∴OE⊥BD,
∵AB=2$\sqrt{2}$,AD=2,∠BAD=45°,
∴BD=$\sqrt{8+4-2×2\sqrt{2}×2cos45°}$=2,
∴AD2+BD2=AB2,∴AD⊥BD,
又AD?平面ADE,OE?平面ADE,AD∩OE=O,
∴BD⊥平面ADE,又BD?平面BDE,
∴平面BED⊥平面EAD.
解:(3)过O作ON⊥AB,垂足为N,则ON⊥OM,
以O为原点,以ON,OM,OE为坐标轴建立空间直角坐标系,如图所示:
则E(0,0,$\sqrt{3}$),G(0,$\sqrt{2}$,0),B($\frac{\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$,0),F(0,$\sqrt{2}$,$\sqrt{3}$),
∴$\overrightarrow{BE}$=(-$\frac{\sqrt{2}}{2}$,-$\frac{3\sqrt{2}}{2}$,$\sqrt{3}$),$\overrightarrow{GE}$=(0,-$\sqrt{2}$,$\sqrt{3}$),$\overrightarrow{BF}$=(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$,$\sqrt{3}$),
设平面BDE的法向量为$\overrightarrow{m}$=(x1,y1,z1),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BE}=0}\\{\overrightarrow{m}•\overrightarrow{GE}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}{x}_{1}-\frac{3\sqrt{2}}{2}{y}_{1}+\sqrt{3}{z}_{1}=0}\\{-\sqrt{2}{y}_{1}+\sqrt{3}{z}_{1}=0}\end{array}\right.$,令y1=$\sqrt{3}$得$\overrightarrow{m}$=(-$\sqrt{3}$,$\sqrt{3}$,$\sqrt{2}$),
∴cos<$\overrightarrow{BF},\overrightarrow{m}$>=$\frac{\overrightarrow{BF}•\overrightarrow{m}}{|\overrightarrow{BF}||\overrightarrow{m}|}$=$\frac{\sqrt{6}}{2×2\sqrt{2}}$=$\frac{\sqrt{3}}{4}$,
设直线BF与平面BED所成角为α,则sinα=|cos<$\overrightarrow{BF},\overrightarrow{m}$>|=$\frac{\sqrt{3}}{4}$.
∴直线BF与平面BED所成角的正弦值为$\frac{\sqrt{3}}{4}$.
点评 本题考查了线面平行,面面垂直的判定,空间向量与空间角的计算,属于中档题.

| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
| A. | (1,$\sqrt{2}$) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | (1,$\frac{2\sqrt{3}}{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
 ,全集U=R。
,全集U=R。 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取范围。
的取范围。 如果满足:①
如果满足:① ;②若对
;②若对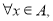 有
有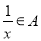 ,则称
,则称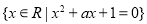 ;
;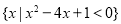 ;
; .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )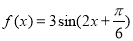 ,给出下列命题:
,给出下列命题: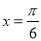 对称
对称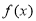 的最大值是3
的最大值是3