题目内容
设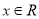 ,函数
,函数 ,
,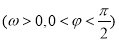 .已知
.已知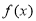 的最小正周期为
的最小正周期为 ,且
,且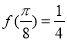 .
.
(1)求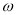 和
和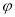 的值;
的值;
(2)求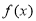 的单调递增区间;
的单调递增区间;
(3)求函数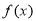 在区间
在区间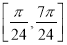 上的最小值和最大值.
上的最小值和最大值.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线y2=12x的焦点重合,且双曲线的离心率等于$\sqrt{3}$,则该双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
9.y=$tan(4x+\frac{π}{3})$的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |


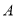 如果满足:①
如果满足:① ;②若对
;②若对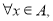 有
有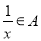 ,则称
,则称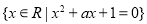 ;
;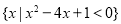 ;
; .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )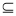 B的B的个数是( )
B的B的个数是( )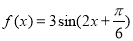 ,给出下列命题:
,给出下列命题: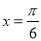 对称
对称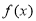 的最大值是3
的最大值是3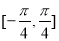
 ,
, ,且
,且 ,则实数
,则实数
 B.
B. C.
C. D.
D.